天才数学者たちはどんな難問に頭を悩ませているのか。NHKの知的エンターテインメント番組「笑わない数学」の放送内容を再構成した書籍より、「BSD予想」についての箇所を紹介する――。（第3回）

※本稿はNHK「笑わない数学」制作班編『笑わない数学2』（KADOKAWA）の一部を再編集したものです。

数学のアイデア
写真＝iStock.com／alexsl
※写真はイメージです
全ての画像を見る（18枚）

超難問BSD予想とはどんな問題なのか

今回のテーマは「バーチ・スウィンナートン＝ダイアー予想」です。この難問を世に送り出した2人の数学者、ブライアン・バーチとピーター・スウィンナートン＝ダイアーに敬意を表して名付けられました。ちょっと長いので、イニシャルをとって「BSD予想」とも呼ばれています。

ブライアン・バーチ
2011年5月4日、ケンブリッジ大学でバーチ・スウィンナートン＝ダイアー予想を説明するブライアン・バーチ（写真＝Fumeinab sakuseir-shau h／CC-BY-3.0／Wikimedia Commons）

このBSD予想、アメリカのクレイ数学研究所が100万ドルの賞金を懸けている「ミレニアム懸賞問題」のひとつなのです。21世紀の数学が向かうべき指針として掲げられたミレニアム懸賞問題については、2024年12月6日配信の「数学史に残る快挙を成し遂げた男は忽然と姿を消した…『決して近づいてはいけない難問』を解いた数学者の現在」でも紹介していますので、そちらもご覧ください。

このBSD予想、数学の問題としてもとっても難しいのですが、まずどんな問題なのか理解することが難しいのです。ですから今回の1つの目標は、BSD予想がどんな問題で、どんな重要性があるのか、それをお伝えしてみたいと思います。

とはいえ、いきなりBSD予想の本丸に切り込むのは荷が重いですから、少し簡単な話から始めていきましょう。

入り口は数学で習った「座標」から

数学が得意であった方、理系の大学に進学した方は覚えているかもしれません。「方程式x²＋y²＝2で表される円周」という用語。いかがでしょうか。「方程式が円周（図形）を表すなんて聞いたことがない」と思う方も少なくないでしょう。

方程式と円（図形）が、どうつながるというのでしょうか？

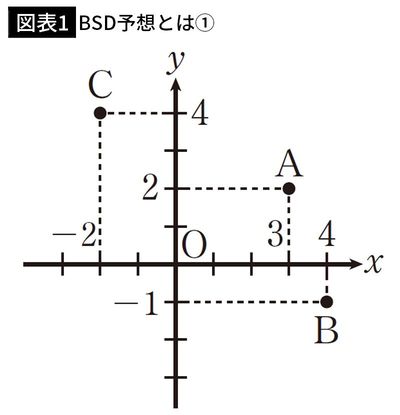
方程式と図形をつなぐもの、それが「座標」です。座標とはある空間内での点の位置を示す住所のようなもので、数の組として表されます。

例えば将棋では、2七歩のように将棋盤のマス目を指定するのに「右から何行目、上から何段目」と表しますが、これと同じように平面上の点を「原点から右にいくつ、上にいくつ動いたか」と表すのです（ただし、数える方向は将棋と逆です）。

【図表1】BSD予想とは①
（『笑わない数学2』より）

このように、数の組と対応づけて点の位置を捉える道具が座標です。座標の発明によって、図形の問題（幾何）を数の組の問題（代数）に、また逆に代数を幾何に結び付けることが可能になりました。

例として、原点O（0，0）を中心とする半径√2の円を考えてみましょう。この円周上の1点の座標をA（a，b）とすると、OA＝√2と、三平方の定理から

a²＋b²＝2

です。これは、方程式x²＋y²＝2にAの座標（a，b）を代入すると、きちんと成り立つことを意味しています。逆に、方程式x²＋y²＝2に代入して成り立つ数の組（a，b）が座標として表す点をすべて集めると、原点Oを中心とする半径√2の円が浮かび上がります。つまり「方程式x²＋y²＝2が表す円周」とは原点Oを中心とする半径√2の円周に他なりません。

今回のテーマ「BSD予想」は、方程式が表す図形に関する超難問なのです。