りんご｢直径8cm1個で150円｣｢直径6cm2個で150円｣どっちが得か…大人も簡単に引っかかる数字トリックの謎【2023下半期BEST5】 答えを言われても納得できない人が続出のワケ

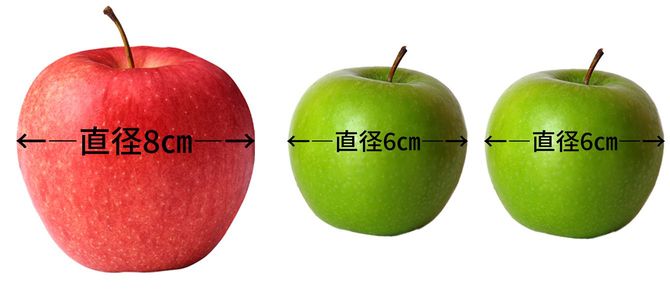
Q3　スーパーに行ったところ、直径8cmのりんご1個と、直径6cmのりんご2個がともに150円で売られていました。量の多さで選ぶなら、どちらを買うべき？（りんごは球体と考えてください）

A　直径8cmと6cmの球体を思い浮かべたとき、見た目の大きさはさほど違いませんから、直感で6cmのりんご2個のほうが断然お得だと感じる人は少なくないのではないでしょうか。

でも、計算してみると8cmのりんご1個のほうが量、つまり体積は大きいのです。球体の体積を求める公式は、「3分の4πr3乗」。πは円周率（3.14）。rは半径で、この場合それぞれ4と3です。計算すると直径8cmのりんごは約268cm³。一方、直径6cmのりんごは約113cm³で2個分だと226cm³になります。

もっと簡単に考えるとするなら、「3分の4πr」までは同じなわけですから、「r」、つまり半径の3乗を比較すればいいのです。4の3乗は4×4×4＝64。3の3乗は3×3×3＝27で、2個分は54です。

（左）写真＝iStock.com／kyoshino（右）写真＝iStock.com／Jonas_ 加工＝プレジデントオンライン編集部

※写真はイメージです

そう言われても、まだ感覚的に納得できない人もいるでしょう。これは人間が物を見るときには2次元の情報としてとらえているために起こる問題です。

面積を計算すれば、円の面積は「πr2乗」ですから、直径8cmのりんごは約50cm²。直径6cmのりんご2個は約56.5cm²と、6cmのりんご2個のほうが大きくなります。薄く輪切りにしたりんごを想像すればわかりやすいでしょう。

『プレジデントFamily 算数が大得意になる 2023完全保存版』（プレジデントムック）

でも、りんごそのものの場合は3次元。奥行きがあるので感覚が変わってくるのです。たとえば物体を奥行きまで計算してきれいに描くには、画家でも訓練しなければなりません。3次元になると人の直感があてにならないのです。

大盛りの料理も同じ。皿の上から見ると2倍ぐらいの量に思えたとしても、実際は2×2×2で8倍もの量が盛られているのです。ですから飲食店で「制限時間以内に全部食べたらタダ。食べきれなかったら支払い」などといううたい文句があったとしても、勝負しないほうが無難です。（答え　8cmのりんご1個）

（以下、後編Q4～6へ続く）

• 【後編】小遣い｢1年目は5000円で年1000円ずつ増｣｢半年で2500円､半年ごと250円増｣どっちが得か…答えに大人も愕然