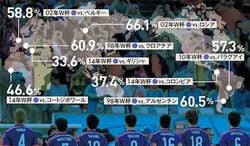
コートジボワール戦は「半沢直樹」なみをキープ ※関東地区の番組平均世帯視聴率のデータ 出所:ビデオリサーチの許諾を得て転載(写真=時事通信フォト)
サッカーのワールドカップ・ブラジル大会で、日本チームは残念ながら1次リーグで敗退したが、日本中を大いに盛り上げてくれた。日本戦の視聴率はビデオリサーチの調査(関東地区)によると、初戦の対コートジボワール戦が最も高くて46.6%。W杯日本戦の過去最高視聴率の66.1%(2002年の日韓大会・対ロシア戦)には及ばなかったが、昨夏の大ヒットドラマ「半沢直樹」最終回の視聴率である42.2%なみだったことからも、W杯の人気ぶりがうかがえる。
ところで、視聴率が46.6%だったのなら、日本人の46.6%もの人々がテレビで観戦したと思うかもしれない。しかし、そうとは限らない。視聴率には統計上の“誤差”があるからだ。
視聴率とは、一般にテレビ保有世帯のうち、どのくらいの世帯がその番組にチャンネルを合わせていたかという「世帯視聴率」を指す。ビデオリサーチの関東地区での調査では、無作為に選んだ600世帯にモニターになってもらい、視聴の状況を調べている。つまり、視聴率46.6%というのは、600世帯のうちの279.6世帯に過ぎない。こうした調査法を、統計学では「標本調査」と呼ぶ。母集団の中から一部のサンプルを抜き出して調査し、その結果から母集団全体の状況を推測するというやり方だ。

ここから先は有料会員限定です。
登録すると今すぐ全文と関連記事が読めます。
(最初の7日間無料・無料期間内はいつでも解約可)
プレジデントオンライン有料会員の4つの特典
- 広告最小化で快適な閲覧
- 雑誌『プレジデント』が最新号から読み放題
- ビジネスに役立つ学びの動画が見放題
- 会員限定オンラインイベント
(野澤正毅=構成 時事通信フォト=写真)





