●×●＝256が解ける子解けない子の差 4つの解法をすぐ思いつくか？

「いろいろな解法を思いつく子こそ賢い」

では、もうひとつ解法を紹介する。

図形問題では＜分ける＞＜全体から引く＞＜移動＞のいずれかを使う確率が高い。次の解法は、図形を分けて、移動させる解き方である。

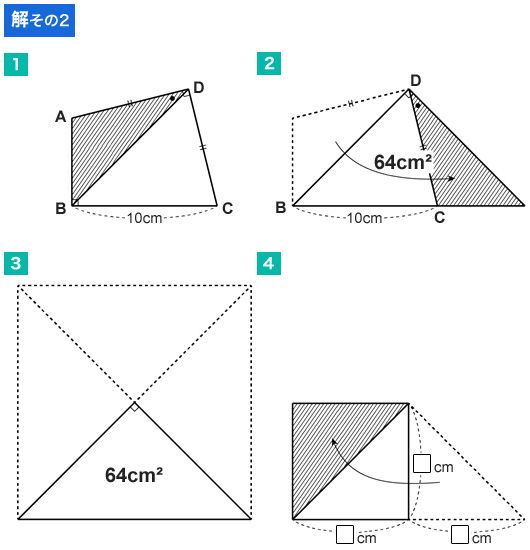
図のように三角形ABCを移動させると、直角二等辺三角形になる（図1、2）。面積が64平方cmの直角二等辺三角形。先ほどの問題の答えと同じだ。

あとは、次のいずれかのアプローチで長さを求めていけばよい（図3、4）。

【図3】64×4＝256　●×●＝256　●＝16cm　16－10＝6
【図4】□×□＝64　□＝8　8×2－10＝6cm　□は辺ABの長さと等しいので、答えは6cm

今回は、簡単な問題を使って、より難度の高い問題を解くことができるような配列にした。過去の問題やこれまで習ったことを「使う」ことで、センスは磨かれる。自分には才能がないからといって諦めることはない。答えにたどり着くためのアプローチを複数考える癖をつけ、「習っていない、知らないからできない」ではなく、「習った（経験した）何と近いのか、何を応用すれば正解にたどり着けるだろうか」と考える訓練が、センスを磨く。

今年、最難関校のひとつと言われる、筑波大附属駒場中学校に合格した生徒のエピソードを紹介したい。小学6年生の彼が質問に来た時は大変だった。

「先生、これを教えてください」ではなく、「先生、ぼくはこう解いたのですが、ほかに良い解き方はありませんか？」だったからだ。

いろいろな解法を思いついてこそ賢い、と授業中に口ぐせのように話し、言葉のやりとりをしていたことが、この6年生だけでなく塾講師の私の成長にもつながったのだ。