11×11=121、12×12=144 ●×●=256は?
冒頭の問題の内容をおさらいしよう。
Q:AD=CD、BC=10cm、四角形ABCDの面積が64平方cmのとき、辺ABの長さは何cmですか。
それでは解説を始めよう。解法は2つ示す。
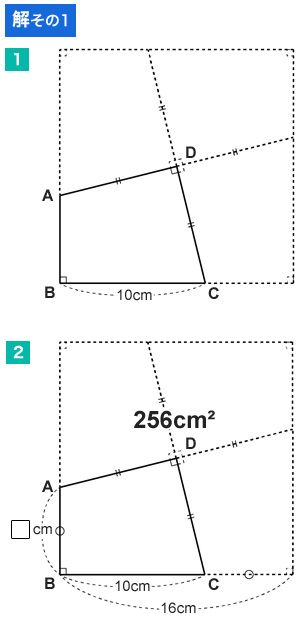
同じ図形を4つ組み合わせると、大きな正方形になる。
64×4=256平方cm
正方形の面積を求める公式は、一辺×一辺なので、
●×●=256 ●=16cm 16-10=6
図の「○」の部分が辺ABの長さと等しいので、答えは6cmとなる。
最初のポイントは●×●=256の●が16とすぐに出ないと解けないということだ。受験生の多くは11×11=121、12×12=144、13×13=169……、16×16=256といった数字が頭に入っている。算数は前述したように、いくつかの解法へのアプローチを思いつくことも重要だが、こうした「基本的な数字」をしっかり覚えておくことも合格への生命線となるのだ。
あるいは、●×●=256の一の位に注目すると良い。256の一の位は「6」。つまり、4×4=16か、6×6=36をヒントに、●は14か16のどちらかだと絞り込みを行うことができる。
この問題のもうひとつのポイントは同じものを4つ組み合わせて正方形を作るという点にある。前出の直角二等辺三角形の問題と同じアプローチである。前出の問題からの応用問題というわけである。
図形問題を繰り返し大量演習させてもセンスは磨かれない。それどころか、ワンパターンの訓練を繰り返せば繰り返すほど、柔軟な思考力は育たなくなり、パターン化された問題やマニュアル化されたことしかできない人になってしまう。
一方、一見異なる問題でも、実はアプローチは同一であるというのは、図形問題に限らない。ビジネスにおける問題解決への道筋でも同じだろう。異なる問題でも、同じ解決へのアプローチが適用できることは小学生のうちから教えておきたい。
問題自体を暗記するのではなく、アプローチを引き出しにいれておくことが重要なのだ。