ビジネスの問題解決では、同じ問題であっても、複数の「解」を提案できるものが勝つ。では複数の「解」を導くには、どうすればいいのか。中学受験を専門にする塾講師の松本亘正氏は、平面図形の難問を解説するうえで、事前にいつくかの「基本」をしっかり教えるようにしているという。松本氏は「解を増やす重要性は、中学受験の合否にも影響する」という。どういうことなのか――。
解ける? 解けない? 中学受験の算数に挑戦
中学受験で難関校突破の鍵となる科目は、算数だ。特に、図形問題は合否に直結する。受験に備える小学生はどんな問題に取り組んでいるのか。今回、大人のみなさんに「平面図形」の問題をいくつかご紹介したい。もし、さっと解けるというのなら、かなりの図形センスの持ち主である。
挑戦いただきたいのは、この問題である。
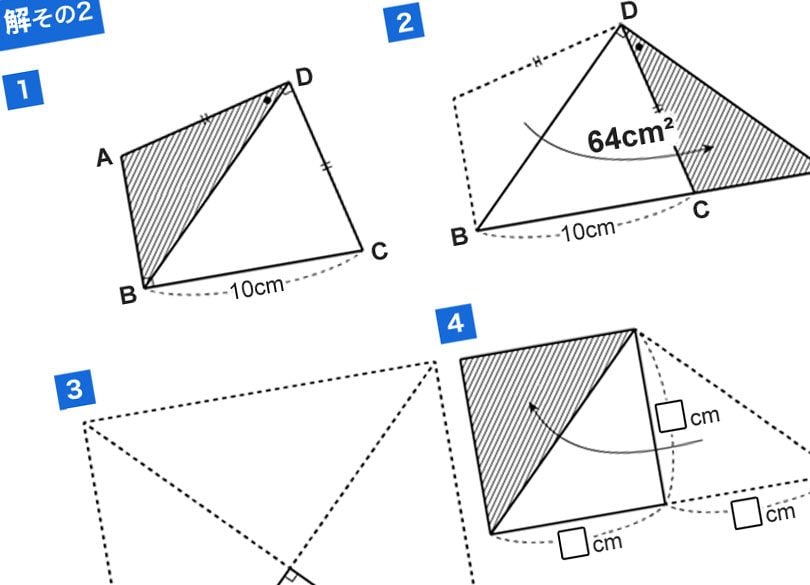
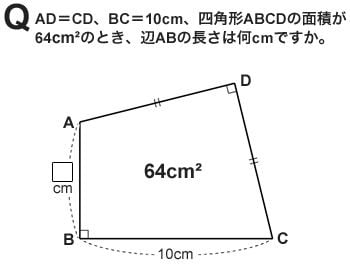
Q:AD=CD、BC=10cm、四角形ABCDの面積が64平方cmのとき、辺ABの長さは何cmですか。
小学生を指導していると、ときおり先天的な資質を感じる子に出会う。どれだけ難しい問題でも、いきなり答えをポンと書いて正解する。ただ、どうやって解いたの? と尋ねても、どういう思考過程で正解できたかの説明は不得手。それでも大人が思いつかないような発想や切り口を考えられるのだ。
もし、わが子にそうした素質を感じるならば、壁にあたるまでは自由にやらせたほうがよい。下手に誘導したり、型にはめたりすると天賦の才能を失わせる危険性があるからだ。
しかし、わが子がある難度になってスランプに陥っている場合や、そもそも図形のセンスがあまりなくて苦労している場合は、今回紹介する方法を参考にしてほしい。