4つの解法を思いつくことができる人1つだけの人
図形のセンスを磨くためには、さまざまなアプローチを試す訓練をさせたほうがよい。その中でどれがベターかベストかまではわからなくてもよい。まずはさまざまな選択肢を思いつくことが大切だ。ビジネスの世界で、多くのソリューションを思いつくことが重要であるのと同じことだ。
小学4年生くらいまで算数が得意だったが、高学年になってつまずいたり、成績が下降線をたどったりする子は、答えが出ることに満足してしまうタイプが多い。特に図形分野は「複数のアプローチを考えられることが賢い」とすりこんでおいたほうがよい。
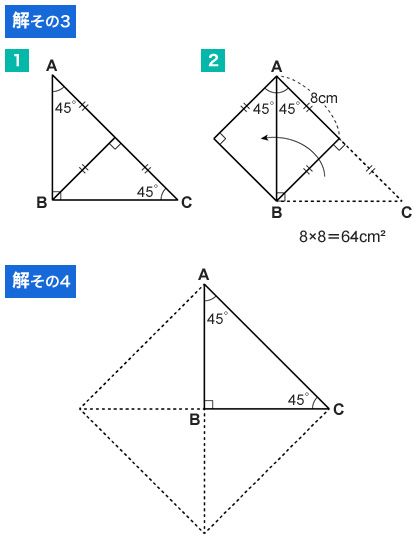
では、残り2つの解法を紹介しよう。解その3である。
解その3は、途中までは解その2と同じだが、最後に正方形を作る解法である。自分が知っている形や把握しやすい形に落とし込んでいる。
最後は、解その4である。解その2では直角二等辺三角形ABCを2つ組み合わせて正方形を作ったが、4つ組み合わせても正方形になる。そして、ACは正方形の一辺となるので、三角形ABCの面積は16×16÷4=64平方cmと求められる。
わざわざ4つも組み合わせるのは非効率だと考える人もいるだろうが、同じものを組み合わせてひとつの形を作るという発想、特に「自分が知っている形や把握しやすい形」にするというアプローチは応用が利くものだ。
では、冒頭の問題の解説に移ろう。簡単な問題の解説をここまで続けてきたのには、もちろん理由がある。