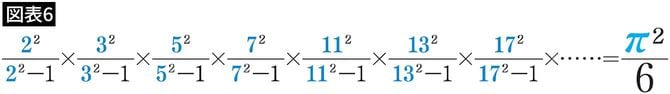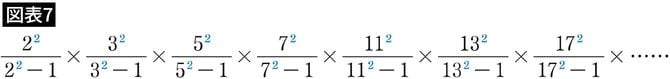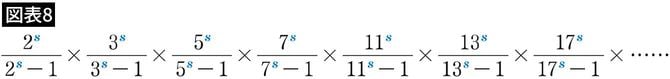2人の天才数学者の挑戦と「意外な発見」
最初に紹介するのは、18世紀を代表するスイス人数学者レオンハルト・オイラーです。オイラーは、まるで息をするかのように計算するといわれた天才数学者です。
素数の並び方の謎に挑むことにしたオイラーは、まず、素数を1つ1つ自分の手で探すことから始めました。
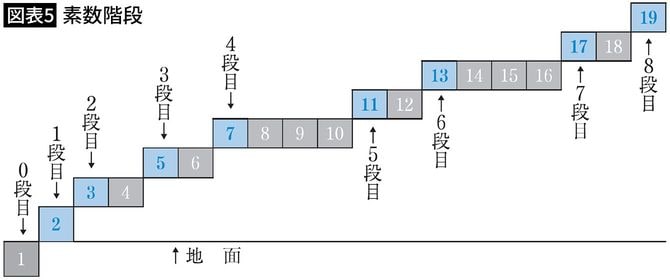
そして頭の中で、素数に出会ったときだけ段があがる階段、いわば「素数階段」を想像してみたのです。
もちろん、パソコンも電卓もない時代でしたので、オイラーは地道に手計算で素数を求めたことでしょう。素数階段の段を踏みしめ、素数が現れるタイミングに何か規則があるのかと、思考を巡らせたはずです。
しかし、オイラーは、素数の並び方の謎を解決することができませんでしたが、素数に関する次の重要な式を発見しました(図表6)。
(左辺が素数だけでできている、ということを覚えていただければ十分です)
そこへ、オイラーと入れ替わるようにして天才数学者カール・フリードリヒ・ガウスが現れます。ガウスは数学史上最大の天才ともいわれ、3歳のときに父親の計算間違いを指摘したという逸話が残されています。
そんなガウスもまた、オイラーがのぼった素数階段を頭の中でのぼり始めました。
そして、ガウスは「ある計算をすれば、素数階段の高さがわかる」と予言したのです。
この予言は、素数の並び方の謎を解決するものではありませんでしたが、「ある数以下の素数が何個あるか」という並び方の謎に迫る大発見でした。
今もなお未解決の難問中の難問「リーマン予想」
オイラーとガウスの発見をさらに進化させる人物が現れます。ドイツの天才数学者ベルンハルト・リーマンです。
リーマンが素数の謎を解くためのヒントにしたのは、オイラーが発見した素数だけでできたこの式でした(図表7)。
リーマンはこの式の肩の数2をsに変えた式「ゼータ関数」を考え始めました(図表8)。
(難しい式ですが、この式も素数だけでできている、ということを覚えていただければ十分です)
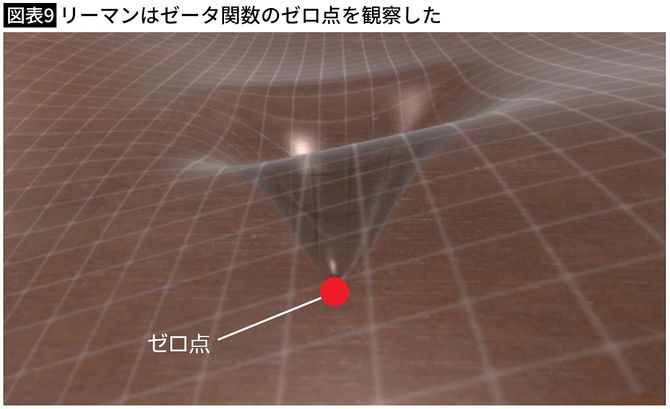
そして、リーマンはこのゼータ関数の大きさを立体的なグラフに描き、グラフの高さが0、つまり「ゼロ点」と呼ばれる点に注目したのです。
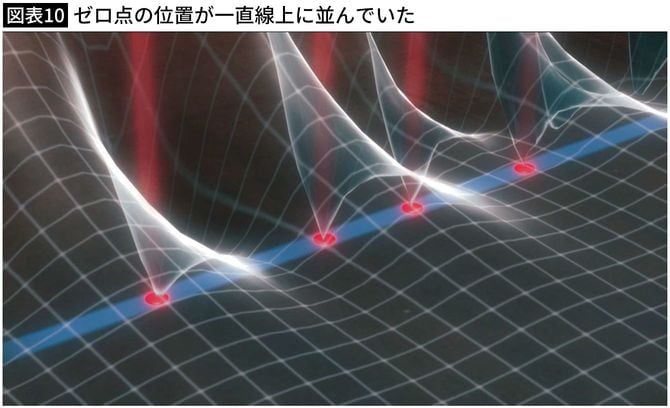
不規則な素数だけで作られたゼータ関数なので、ゼロ点もあたり一面ばらばらに散らばっているかと思われましたが、3つほどゼロ点を求めたリーマンは、ゼロ点の位置がぴたりと一直線上に並んでいることに気づいたのです。
そして、リーマンは、今もなお未解決の難問中の難問であり、最も重要だといわれている「リーマン予想」を予想したのです(図表11)。