多くの数学者を悩ませてきた「四色問題」とはどのようなものか。パンサー尾形貴弘が難解な数学の世界を大真面目に解説するNHKの知的エンターテインメント番組「笑わない数学」の放送内容を再構成した書籍より、一部を紹介する――。

※本稿は、NHK「笑わない数学」制作班編『笑わない数学』（KADOKAWA）の一部を再編集したものです。

「少ない数の色」で地図を塗り分ける方法

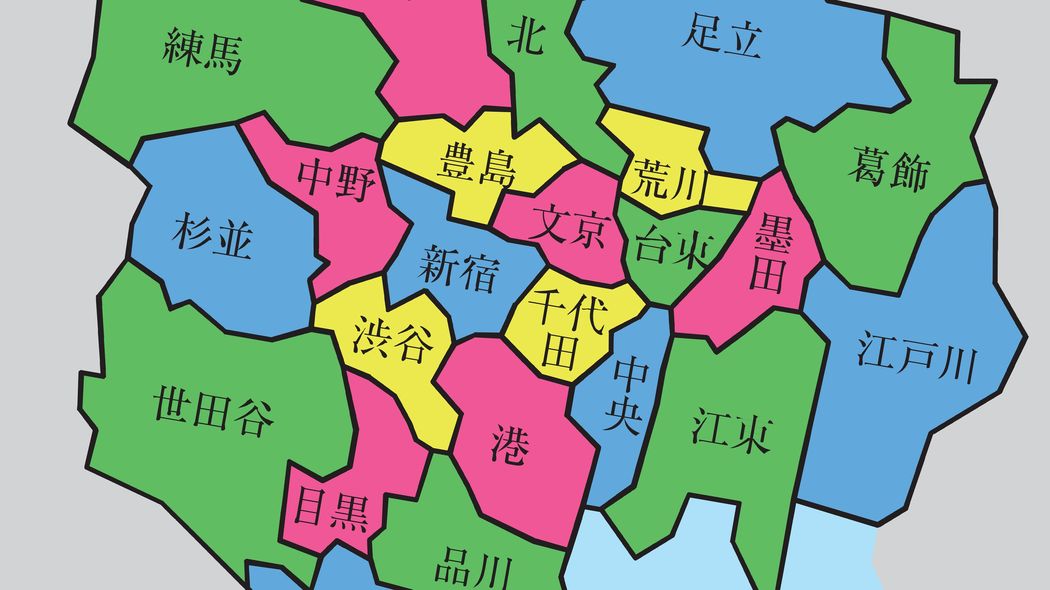
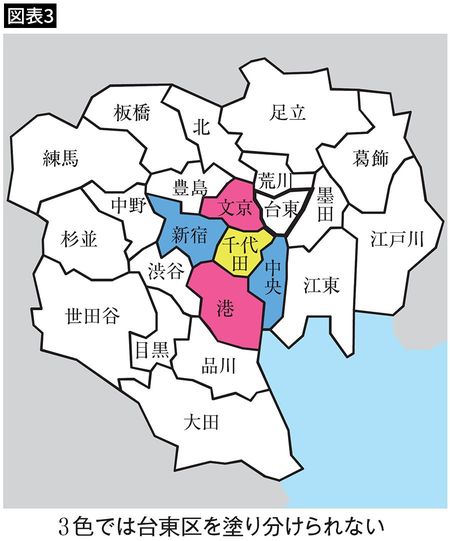
次の図は東京23区の地図です（図表1）。

【図表1】東京23区の地図
出所＝『笑わない数学』
全ての画像を見る（16枚）

これから、この地図を隣の区が同じ色にならないように塗り分けていきます。ただし、できるだけ少ない数の色で塗り分けます。

まずは、赤と青の2色で塗り分けられるかみてみましょう。

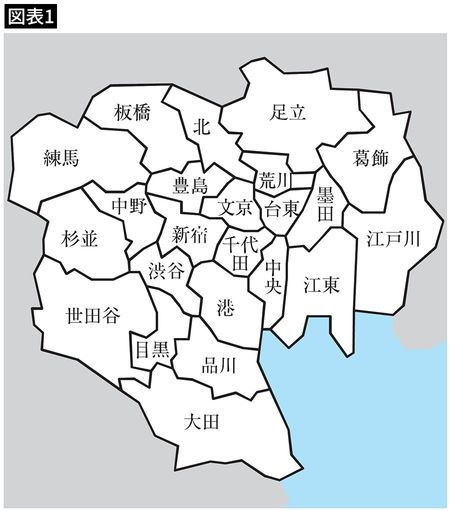
港区を赤、中央区を青で塗ると、両方の区に隣接する千代田区は赤でも青でも塗り分けることができません（図表2）。

【図表2】2色で塗り分けられるか試した東京23区の地図
出所＝『笑わない数学』

それでは、赤色と青色に黄色を加えた3色であればどうでしょうか？　千代田区を黄色で塗ることができます。

そして、新宿区は港区と千代田区に隣接するので青色、文京区は千代田区と新宿区に隣接するので赤色に塗り分けることができます。

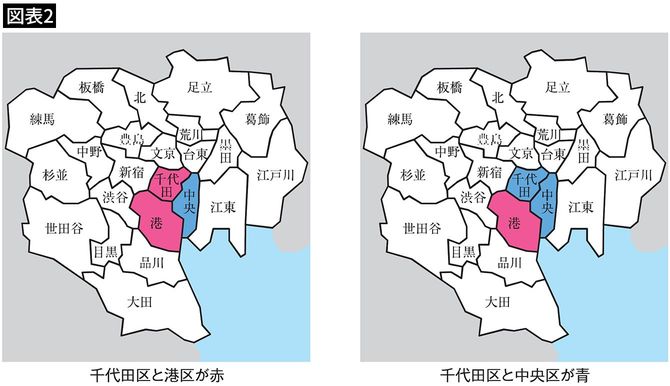
すると、台東区は中央区、千代田区、文京区の3区に隣接するため、赤でも青でも黄でも塗り分けることができません（図表3）。

【図表3】3色で塗り分けられるか試した東京23区の地図
出所＝『笑わない数学』

それでは、赤色、青色、黄色に緑色を加えた4色あればどうでしょうか？　台東区を緑色で塗ることができます。

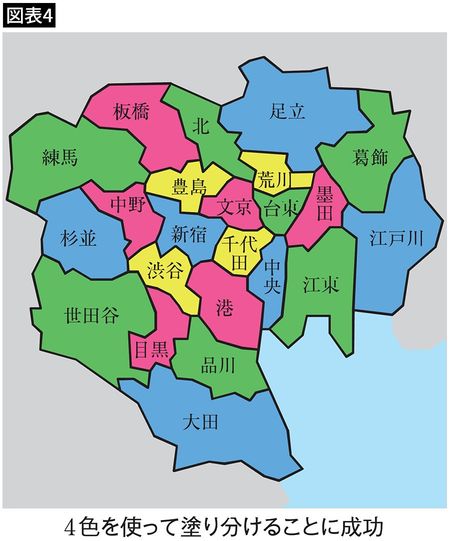
さらにどんどん塗り分けていくと、4色あれば東京23区をすべて塗り分けることができました（図表4）。

【図表4】4色で塗り分けた東京23区の地図
出所＝『笑わない数学』

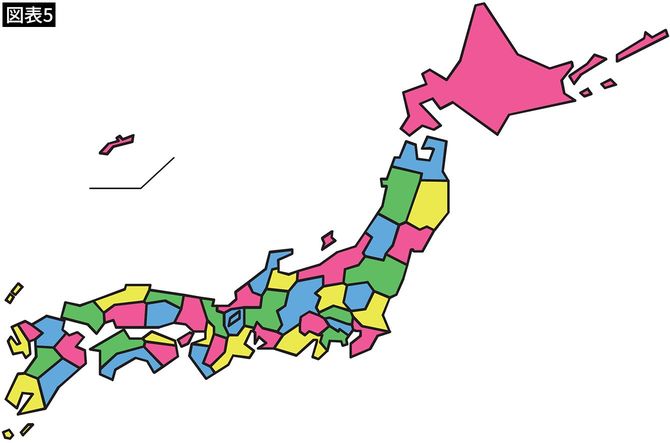
同じように、日本地図も4色で塗り分けられます（図表5）。

【図表5】4色で塗り分けた日本地図
出所＝『笑わない数学』

世紀の難問「四色問題」とは

これまでの説明で「四色問題」がどのような問題か、おわかりいただけたのではないかと思います。

そうです。世の中のすべての地図は、4色あれば塗り分けられるのではないか、それをどうやったら証明できるのかが、世紀の難問「四色問題」なのです。

この問題は、1852年イギリスのロンドンで、ある若者が「どんな地図でも4色で塗り分けることができそうだ」と気がついたことから始まったと言われています。

その話を聞いたイギリスを代表する数学者の一人、オーガスタス・ド・モルガンは、このことを数学的に厳密に証明しようと思い立ちます。

しかし、ド・モルガンは証明に大苦戦。彼が学者仲間にこの難問をなげかけていったことで、四色問題は世に広まっていったのです。

ド・モルガン以外にも多くの数学者が四色問題に挑戦しましたが、誰も証明には到達できず、時間だけが流れていきました。

しかし、問題が生まれて27年後の1879年に四色問題を大きく前進させる論文が発表されました。

その論文の著者はアルフレッド・ケンプというロンドンで働く弁護士でした。