数学の本質は､その自由性にあり…｢普通の無限｣と｢でっかい無限｣をみつけた天才カントールのすごい発想 ｢究極の自由人｣が数学界のタブーを打ち破った

※本稿は、NHK「笑わない数学」制作班編『笑わない数学』（KADOKAWA）の一部を再編集したものです。

写真＝時事通信フォト

「ツール・ド・東北　2019」記者発表会に出席した、（左から）お笑いトリオ「パンサー」の菅良太郎さん、向井慧さん、尾形貴弘さん（2019年5月14日、東京都）

全ての画像を見る（8枚）

数学の世界では気軽に登場する「無限」

皆さんは「無限」と聞いて何を想像するでしょうか？

とても大きいこと？　とてもたくさんあること？　あるいは、文字通り「限りが無い」こと？

でも、とてもたくさんって、どれくらい？　限りがないって、どういうこと？

考え出すとわからなくなる無限ですが、数学の世界では無限が気軽に登場します。私たちにとって身近な、1，2，3，……と並ぶ「自然数」すら、限りなく続く不思議な数です。

では、ここでクイズです。

無限にある自然数1，2，3，……の個数をなんらかの方法で数えたとします。

同じように、無限にある偶数2，4，6，……の個数も数えたとします。

直感的には、自然数の方が大きそうですよね。自然数には偶数以外の数が含まれていますから。たとえば、3は自然数ですが偶数ではありませんので、自然数の方が大きいように思えます。

「無限」を比べるためのシンプルな方法

でもおかしくないですか？　偶数は無限にあるのに、それよりも「多い」ものがあるなんてこと、あり得るのでしょうか？　偶数より多いものがあるのなら、偶数には「限りがある」＝「無限じゃない」ってことになってしまいますよね？

では、このクイズについて考えてみましょう。方法は簡単です。偶数を先頭から数える、つまり自然数と結びつけていけばよいのです。

出所＝『笑わない数学』

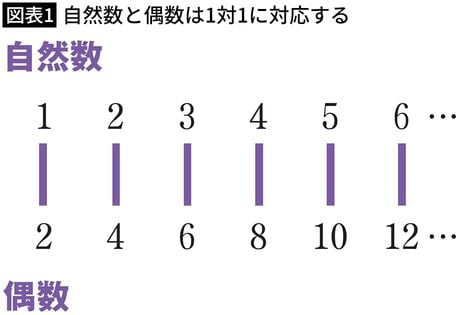
2は最初の偶数なので1と結びつきます。4はその次の偶数なので2と結びつきます。6は3と、8は4と、……といった調子でどんどん結びつけていくと、すべての自然数と偶数が1対1に結びつき、1個たりとも余りません。

よって、自然数と偶数はどちらも同じ大きさであることがわかりました。

このように、「ひとつずつ結んでいって、余りがなければ同じ個数」という、ごく自然な考え方を使って、無限を比べることができるのです。