最後の関門「五辺国」
四辺国を含む地図まで4色で塗り分けられることがわかったのですから、残るは五辺国をひとつでも含むn+1カ国の地図が4色で塗り分けられるかどうかです。
ケンプは1879年に発表した論文で、そのことを証明しましたが、その11年後に誤りであることが見つかります。
ケンプの方法では証明できないということがわかった後、多くの数学者たちが新しいアイデアを用いて証明に挑んだものの、長い間誰一人成功しませんでした。
しかし、20世紀にはいると、そんな絶望的な状況に僅かな希望を与える新たな証明方法が考案されます。
その方法とは、五辺国を含む地図をさらに細かく分類して、塗り分けられるか調べてみようというものです。
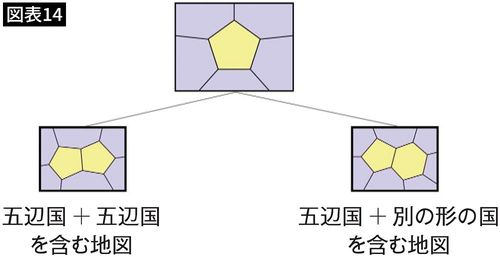
実は、五辺国を含む地図は、さらに次のように2つに分類できるのです(図表14)。
分類した2つをそれぞれ4色で塗り分けられることを証明できれば解決です。
しかし、この方法でも、誰も証明にたどり着くことはできませんでした。
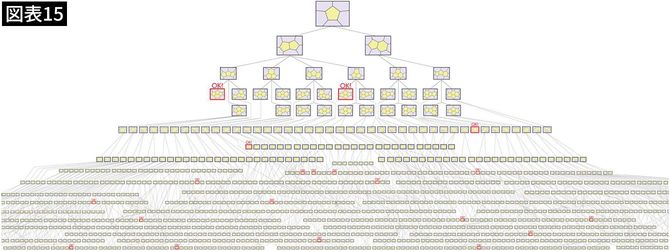
数学者たちは、さらに分類を行い、それでも駄目ならさらに分類することを繰り返すことになりました。
この方法で、4色で塗り分けられる分類をいくつか見つけることができたのですが、爆発的に増えていく分類は段々と手に負えなくなっていきました。
エレファント(elephant)な証明による決着
この作業はいつ終わるのか? そもそも終わりはあるのか? こうして四色問題の証明は人間には到達できない無謀な挑戦だと恐れられるようになっていきました。
四色問題が生まれて1世紀以上が過ぎた1970年代に、アメリカの数学者ウォルフガング・ハーケンとケネス・アッペルが、コンピュータで膨大な証明作業に挑んだのです。
そして、コンピュータを用いた計算開始から4年後、遂にコンピュータが証明の完了を告げます。
実に124年の時を経て、四色問題は解決されました。
しかし、この証明は批判を浴びてしまいます。
当時の数学者は、コンピュータによる証明に馴染みがなかったため懐疑的な声があがったのです。
さらに、ひたすら分類を行う証明スタイルは泥臭すぎて「美しくない」とも言われ、「エレガントな証明」(elegant proof)を期待していた人からは「エレファントな証明」(elephant proof)と言われてしまったのです。
今ではコンピュータを使う証明も立派な証明方法とされています。しかし一方で、人間が本来持つ知性の底力を見せつけるような「エレガントな証明」が期待されているのも、また事実なのです。