東京23区を｢最も少ない色｣で塗り分けるには何色必要か…解決まで124年もかかった数学の超難問を解説する 最終的な証明は｢エレファントな証明｣になった

「箱に入った地図を4色で塗り分けられるか」

ケンプはまず、ありとあらゆる地図を「国の数で地図を分類する」ことから始めました。それはつまり、下の図のように、1カ国の地図すべてが入った箱、2カ国の地図すべてが入った箱、……、100カ国の地図すべてが入った箱、……、10000カ国の地図すべてが入った箱、……とすべての地図を国の数で分類したのです（図表6）。

出所＝『笑わない数学』

そして、それぞれの箱に入った地図が4色で塗り分けられるか考えたのです。

1カ国の地図たちは当然4色で塗り分けられますよね。1カ国しかない地図なのですから、4色のうちどれかの色で塗ってしまえば塗り分けられます。

つまり、1カ国の地図すべてが入った箱は4色で塗り分けOK。

同じように、2カ国の地図すべてが入った箱も、3カ国の地図すべてが入った箱も、4カ国の地図すべてが入った箱も4色で塗り分けOKということがわかります。

難問解決のカギとなる仮定

では、この調子で5カ国すべてが入った箱、6カ国すべてが入った箱、……も4色で塗り分けOKと証明できるでしょうか？　もしかしたら塗り分けOKと証明できるかもしれません。

ただ、何カ国の地図まで塗り分けられるかわからないので、とにかく1カ国の地図すべてが入った箱から、nカ国の地図すべてが入った箱までが4色で塗り分けOKになったと仮定したのです。

そして、ケンプはこんなことを言いました。

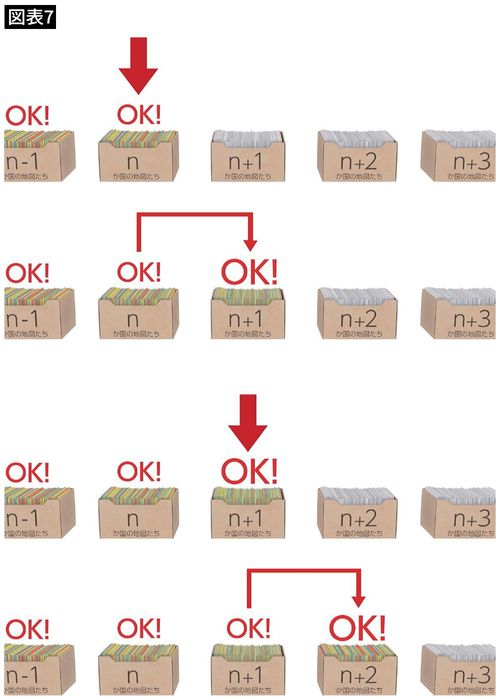
もし、ケンプの言っている“都合の良いこと”が本当にあるのなら、nカ国までの箱が全部OKだということから、n＋1カ国の箱も自動的に全部OKということになります。

そして、さらに“都合が良いこと”によってn＋2カ国の箱も自動的にOK、n＋3カ国の箱もOK、……というように、まるでOKサインのバケツリレーのように、無限に続くすべての箱がOKだということがいえてしまいます。

出所＝『笑わない数学』

つまり、この“都合が良いこと”が実際にあることが示せれば、四色問題は解決できるのです。