｢665×781は何か｣と聞かれて｢大体520000｣と瞬時に答えられる人が頭の中でやっている"シンプルな計算方法" ｢36×12は何か｣と聞かれて｢432｣と正確な答えを出す意味はない (5ページ目)

「テキトー」でいいとわかれば計算が楽しくなる

この方法で計算をしてみると、ちょっと驚くほど近い数字が出てくるようになるのではないでしょうか。すると、計算することが楽しくなってきて、周りの数字を何でも計算してみたくなってくるはずです。

斎藤広達『頭のいい人が使っているずるい計算力』（PHP研究所）

そうなったら、しめたものです。日常的に計算を繰り返すことで、あなたの「ざっくり暗算力」は確実に高まっていくからです。

大切なことは、最初から細かい計算をしようとするのではなく、まず概算の値を出して、その後それを調整する、ということです。

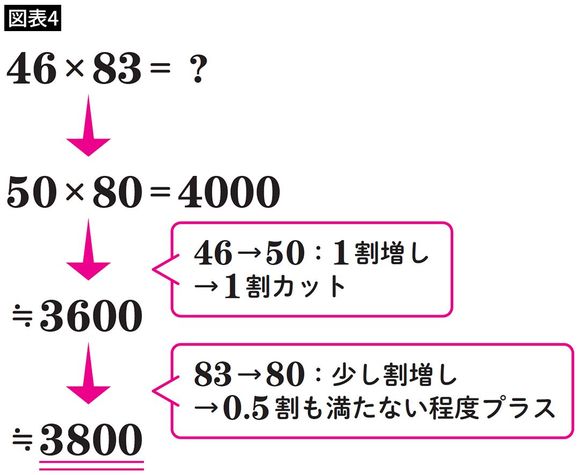
その考え方さえ身につければ、46×83などという計算も、

「とりあえず四捨五入して50×80にしよう。4000だな」
「46を50にしたということは、だいたい1割増しだな。じゃあ代わりに1割カットか。3600くらいだな」
「83を80にカットしたというのは誤差の範囲かもしれないけど、ちょっとだけ割り増しして、3800にしておくか」

とすれば、大まかな数値は得られます（正確な答えは3818）。

出所＝『頭のいい人が使っているずるい計算力』（PHP研究所）

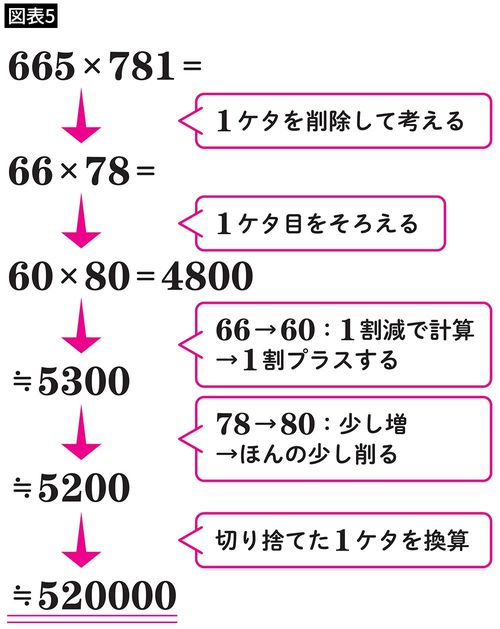
あるいは、665×781などというより位の多い計算も、

「下1ケタは不要だな。66×78で十分だ」
「まずは60×80で計算してみよう。4800だな」
「66を60にしたわけだから、1割くらいプラスしておこう。だいたい5300といったところか」
「78を80にしたから、ほんのちょっと削っておくか。じゃあ5200で」
「切り捨てた下1ケタを換算して、520000だな」

と、徐々に正確な数値に近づいていけるわけです（正確な答えは519365）。

正直に言えば、私は「1ケタ同士の掛け算」にまで単純化してしまっても、実際に問題になることはあまりないと思っています。