図を拡大
「傾き」という言葉にピンときた方はもうおわかりでしょう。そうです。2つのグループを分断する線は一次関数の式で表されます。これを「線形判別分析」といい、文字通り2つのグループを分ける最適な一次関数のモデルをつくるということです。
ここでは、「重回帰分析」を使った簡単な方法で計算してみましょう。
重回帰分析は多変量解析のひとつで、1つの目的変数を複数の説明変数で予測する手法です。
目的は、投資継続と株式売却の判別ですから、投資継続に対するイエス・ノーが目的変数となります。
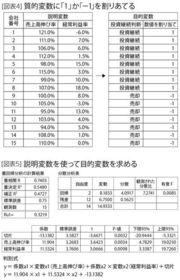
ただ、イエス・ノーのままでは計算ができないので(統計ではこうした変数を質的変数と呼びます)、イエスを正、ノーを負とし、1とマイナス1をそれぞれに割り当てます(図表4)。
次に、2つの説明変数(売上高伸び率と経常利益率)とイエス・ノーとの関係づけを重回帰分析によって導きます。計算結果は図表5のとおりです。
目的変数は2つの説明変数によって、次のような式で求めることができます。
図を拡大
y(目的変数)=11.904×説明変数1(売上高成長力)+11.5234×説明変数2(収益力)-13.1382。
yが正の数値の場合は投資継続、負の場合は売却と判断します。
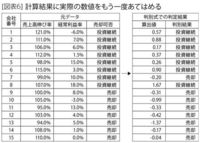
この式に実際の数値をもう一度代入して、投資継続の可否を検証してみます。
1社のみ実際の投資判断と異なった結果となりましたが、「この判別モデルは使える」と、細野さんは検証データを見て大いに満足しました(図表6)。




