統計を学びたいけれども、数式アレルギーが……。そんなビジネスパーソンは少なくありません。でも、大丈夫。日常よくあるシーンに統計分析の手法をあてはめてみることで、まずは統計的なモノの見方に触れるところから始めてください。モノの見方のバリエーションを増やすことは、モノゴトの本質を捉え、ビジネスのための発想や「ひらめき」をつかむ近道です。
統計という手法は、全体を構成する個が数えきれないほど多いとき、「全体から一部分を取り出して、できるだけ正確に全体を推定したい」という思いから磨かれてきた技術といってよいでしょう。
たとえば「標本抽出(サンプリング)」は、全体(母集団)を推定するための一部分(標本)を取り出すための手法です。ところが、取り出された部分から推定された全体は、本当の全体とまったく同じではないので、その差を「誤差」という数値で表現します。では、どの程度の「ズレ」であれば、一部分(標本)が全体(母集団)を代表しているといえるでしょうか。
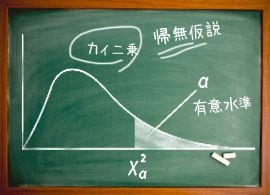
ここでは、「カイ二乗検定」という統計技法を通して、「ズレの大きさ」の問題について考えてみます。
その前に、ちょっとおもしろい考え方を紹介します。その名は「帰無(きむ)仮説」。
C女子大に通うAさんとBさんはとても仲がよいので有名です。
彼女たちの友人は「あの2人は性格がよく似ているから」と口をそろえて言います。本当にそうでしょうか?
これを統計的に検討してみましょう。手順はこうです。
まず、「2人の仲がよいのは性格とは無関係」という仮説を立てます。そのうえでこれを否定することで、「性格がよく似ているから仲がいい」という元の主張を肯定します。
元の主張が正しいと考える立場に立てば、この仮説はなきものにしたい逆説です。そこで無に帰したい仮説ということで、これを「帰無仮説」と呼びます。
「え? 何を回りくどいこと言ってるんだ!」と叱られそうですが、もう少しがまんしてください。
わかりにくいので、もう一度はじめから考えてみます。検定したい対象は、「2人の仲がよいのは性格が似ているから」という友人たちの考えです。

(図表1)図を拡大
前述したとおり、まず「仲のよさと性格の類似性は関係がない」という仮説(帰無仮説)を設定します。
次に、女子大生100人に、「仲がよい人と自分の性格には類似性があると思いますか」「仲が悪い相手と自分の性格は似ていないことが多いですか」という設問を設定し、それぞれについてイエス・ノーで回答してもらいました。
結果は図表1のとおりです。結果を見るとどうやら関係がありそうですね。