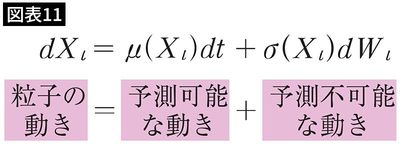「3つの扉の問題」の答え合わせ
最初に紹介した次の問題(図表8)について、そろそろ答え合わせをしましょう。
この問題は1990年9月9日、あるアメリカの雑誌のコラムに掲載されたことで、大きな話題となりました。コラムを書いたのは、IQ228の天才タレントとして人気だったマリリン・ヴォス・サヴァント。そのコラムに寄せられた質問が、この問題だったのです。
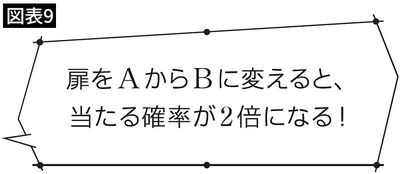
そして、この質問に対して、マリリンはこう答えました(図表9)。
このコラムが掲載されると、全米で大論争が発生。その答えは間違っている、と1万通を超える投書が殺到しました。その中には、有名大学の教授や数学者もいたそうです。
単純に考えたら、マリリンの答えは間違っている気がしますよね。2つ残った扉のどちらかが正解なのですから、扉を変えようが変えまいが、当たる確率は同じはずなのです。
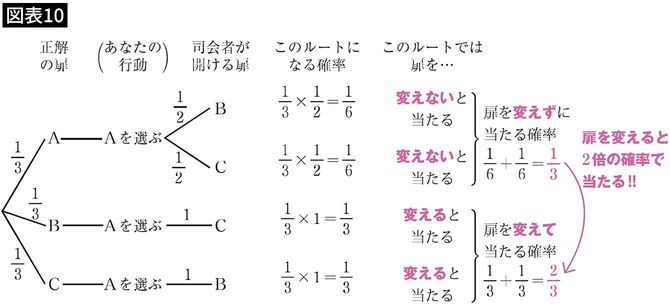
では、あなたが扉Aを選んだ前提で、すべての行動パターンを書き出して考えてみましょう。
商品が扉Aにある場合、司会者はハズレの扉BかCのどちらかをランダムに開けます。この場合は、扉を変えない方がよいですよね。
では、商品が扉Bにある場合、司会者はハズレの扉として必ずCを開けます。この場合は、扉を変えたほうがよいですよね。
そして、商品が扉Cにある場合、司会者はハズレの扉として必ずBを開けます。この場合も、扉を変えたほうがよいですよね。
よって、扉を変える場合の当たる確率は3分の2、変えない場合の当たる確率は3分の1なので、扉を変えた方が2倍の確率で当たるといえるのです!(図表10)
「まだ見ぬ未来」「ランダムな現象」を予測する
ギャンブルから始まった確率論ですが、時を経るうちに少しずつそこから切り離されていきます。そして20世紀、まだ見ぬ未来やランダムな現象を可能な限り予測することを目指した「現代確率論」へと進化を遂げるのです。
きっかけのひとつとなったのは、相対性理論で有名な物理学者アルベルト・アインシュタインが発表した、ブラウン運動に関する論文です。
ブラウン運動とは、ごく小さな粒子が液体や気体の中で不規則に運動する現象のことです。例えばコーヒーにミルクを入れると、ミルクは不規則に広がっていきますが、これはブラウン運動によるものです。
この粒子の動きはあまりに複雑なので、予測が不可能だと考えられていましたが、アインシュタインは、1つ1つの動きは予測できなくても、全体でみるとどのあたりに広がっている確率が高いかを示す法則を見つけ、数式に表したのです。
その後、世界中の数学者たちの研究により、次の数式が発見されます(図表11)。
この方程式が解ければ、ランダムな粒子の動きが予測できるはずだと考えたのです。