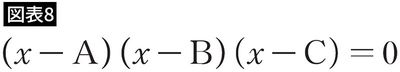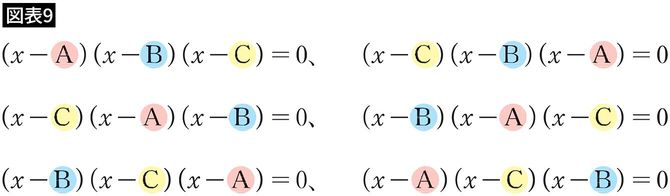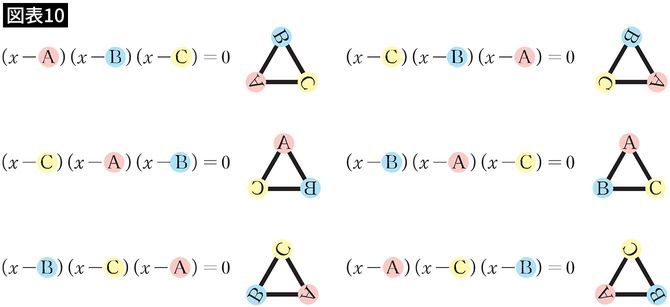2つの図形は「同じ対称性をもつ」

さらに「まったく動かさない」という操作も回転の1つと考えることにします。まったく動かさないのですから、もちろん見た目は変わりません。

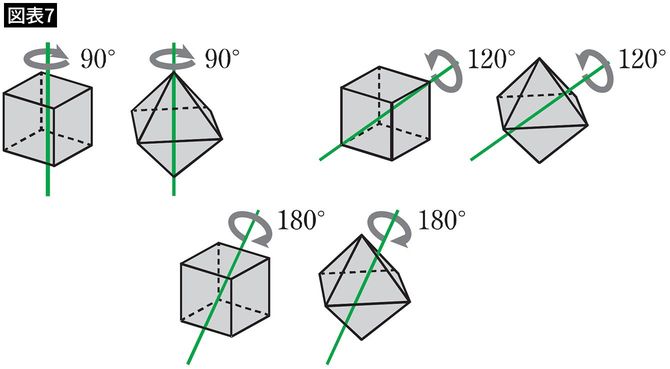
これらの回転（全部で24通り）によって見た目が変わらないこと、それを立方体のもつ対称性といいます。

では、立方体とはまったく異なる図形である正八面体がもっている対称性は、どんなものでしょうか？　実は正八面体は、立方体と同じ軸のまわりに同じ角度だけ回転させても、まったく見た目が変わらないのです（図表7）。

【図表7】正八面体は、立方体と同じ軸のまわりに同じ角度だけ回転させても見た目が変わらない
出所＝『笑わない数学』

このようなとき、2つの図形は「同じ対称性をもつ」といいます。

原始時代にまったく異なるものから共通する数を発見したように（数学の夜明け）、人類はまったく異なる図形から、それらに共通する対称性を発見していったのです（もうひとつの数学の夜明け）。

だからどうした？　と思われるかもしれませんが、これこそが現代数学につながる大進歩だったのです。

そして、このもうひとつの数学の夜明けは、図形だけの話にとどまりませんでした。なんと数学者たちは「図形と、まったく別物であるはずの方程式との間にも、共通する対称性がある」と気付いたのです。

図形と方程式との間に「共通する対称性」

「図形と方程式との間に、共通する対称性がある」とはどういうことなのでしょう。

答えから言ってしまいましょう。

1本の棒のような図形は2次方程式と同じ対称性を、正三角形は3次方程式と同じ対称性を、そして正四面体は4次方程式と同じ対称性をもっています。

そんな事実に、数学者たちは気づいていったというのです。

もう少し詳しくみてみましょう。

ある3次方程式の3つの解をA、B、Cと表すと、その方程式は

【図表8】ある3次方程式の3つの解をA、B、Cと表したときの式
出所＝『笑わない数学』

と表すことができます（図表8）。解を並べ替えることで、この方程式は6通りの表示をもちます（図表9）。

【図表9】6通りの方程式
出所＝『笑わない数学』

正三角形の3つの頂点を同じようにA、B、Cと名付けるとき、これら6つの式に対応するように正三角形を置き換えてみましょう（裏返しもあります）。

【図表10】3次方程式の解の並べ替えと、正三角形の置き換え
出所＝『笑わない数学』

どうでしょうか？　3次方程式の解の並べ替えと、正三角形の置き換えとがぴったり対応していますね（図表10）。