「公式」を盗まれ激怒、数学決闘へ

どうしても秘密の解の公式を知りたいカルダーノは、まずタルタリアを言葉巧みに説得して公式を教えてもらいます。

さらに4年後、今度はデル・フェッロのもとを訪ね、計算ノートを見せてもらいました。

そして、カルダーノは勝手に解の公式を載せた本を出版してしまったのです。3次方程式は「カルダーノの公式」と呼ばれるようになってしまいました。ついには、カルダーノの弟子フェラーリが、タルタリアの考えを参考に4次方程式の解の公式を発見し、タルタリアにとってはまさに踏んだり蹴ったりでした。

公式を盗まれ激怒したタルタリアはカルダーノ一派に数学決闘での決着を申し入れますが、大敗北！　仕事を失い一文無しとなって、非業の死を遂げたと伝えられています。

ともあれ、3次方程式と4次方程式の解の公式は16世紀に相次いで発見されました。それならば、5次方程式や6次方程式の解の公式も、きっと誰かによって発見されたに違いない、そう思いますよね。

ところが、あろうことか、カルダーノの時代から300年経っても、誰も発見できなかったのです。

5次以上の方程式の解の公式はなぜ見つからないのか？　その背景に、いったいどんな秘密が隠されているのか？　その秘密をはっきりと解き明かしたのが、ガロア理論なのです。

そして、それは、人類史上に刻まれた「もうひとつの数学の夜明け」とでも呼ぶべき、知の大変革でもあったのです。

2つの「数学の夜明け」とは

最初の数学の夜明けとは何なのか振り返ってみましょう。

歴史が始まるはるか以前、わたしたちの祖先は、たとえば3個のリンゴと、杭に3回巻かれたロープを目にしていたことでしょう。この2つの全く異なるものですが、人類はそこに共通する「3」という「数」を発見したのです。

同じように人類は、身の回りのさまざまなものから、次々と数を発見していきました。数の発見によって、さまざまな量を表して比べられるようになり、また足したり引いたりと計算が可能になりました。

これこそが、最初の数学の夜明けだったと考えられています。

数の発見をした人類は、「もうひとつの数学の夜明け」とでも呼ぶべき大発見と出会います。今度は、まったく異なる形の間から「対称性」という共通点を発見したのです。

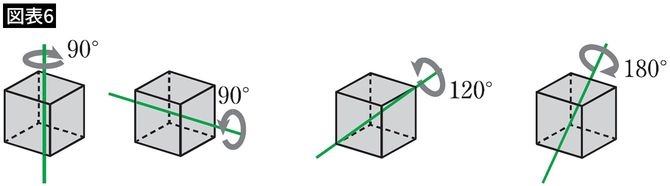
「対称性」とは図形の見た目を変えない動かし方のことです。

たとえば立方体なら、次の図のように、ある軸を中心に何度か回転させても見た目が変わりません（図表6）。

【図表6】ある軸を中心に何度か回転させても見た目が変わらない
出所＝『笑わない数学』