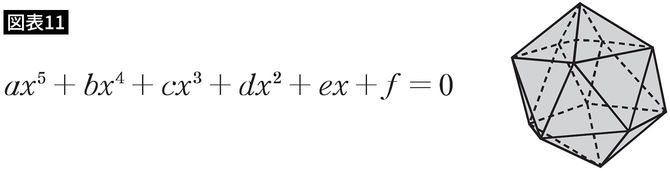｢20歳の革命家の遺書｣が現代数学の歴史を変えた…世界中の数学者の度肝を抜いた｢ガロア理論｣の斬新さ 問題の裏側に回り込み､ハッキングした

「どんな方程式にも解の公式はあるのか？」の解決

さて皆さん、思い出してください。問題は

でした。

実は、5次方程式は、次のちょっと複雑な図形と同じ対称性をもっているのです（図表11）。

出所＝『笑わない数学』

ガロアが登場するのはここから。

かつてカルダーノの時代、数学者は3次方程式や4次方程式をあれこれ変形することで、解の公式を探し求めていました。これはいわば、行き当たりばったり的な方法です。

しかしガロアは、まったく発想を転換して

と見抜いたのです。

ガロアが発見した対称性の謎についてビジュアル化してみました。

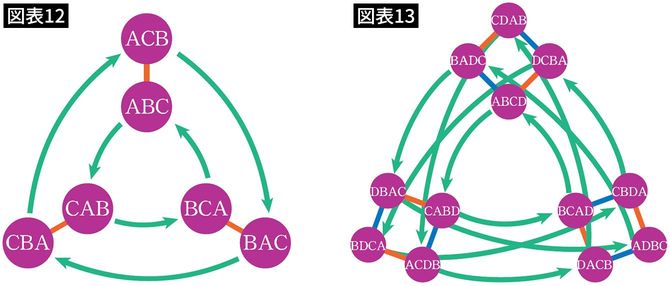
次の図は3次方程式がもつ対称性（図表12）、4次方程式がもつ対称性（図表13）のそれぞれの構造をビジュアル化したものです。

出所＝『笑わない数学』

細かいことはさておき、丸い玉が、いわば分身の術を使ったように規則的な図を形作っているように見えますよね？

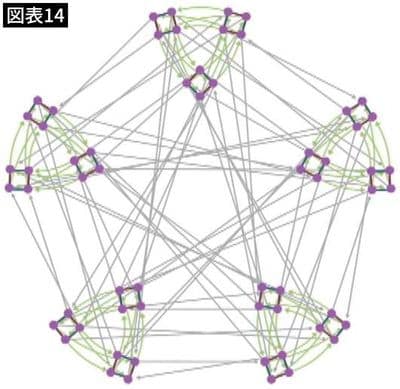
そして、次の図は5次方程式がもつ対称性の構造をビジュアル化したものです（図表14）。

出所＝『笑わない数学』

上の方の一部には分身の術を使った美しい動きもありますが、全体ではなんだかバラバラでまとまりがありません。5次方程式がもつ対称性の構造は、どうやっても規則的で美しい動きをするビジュアル化ができないのです。

ガロアが発見したこと、それはいわば

という事実だったのです。

ガロアが画期的だったのは、方程式を直接いじくるのではなく、それぞれに対応する図形の対称性を調べることで、解の公式があるのかないのかがわかるということでした。

言ってみればガロアは、問題の裏側に回り込み、問題をハッキングするハッカーみたいなやつだった、ということなんです！

天才数学者・ガロアの短く不遇な人生

画期的な数学理論を生み出し、その後の数学に大変革を引き起こしたガロア。

しかし、その自由奔放な天才ぶりは、あまりに斬新な考え方を持っていたことが影響し、人生は短く不遇なものとなってしまいました。

ガロアが初めてガロア理論につながる論文を執筆したのは17歳のときでした。ガロアはその論文を、数学の大御所たちが所属するフランスの科学学士院に二度にわたって提出しましたが、二度とも紛失を理由に受理されませんでした。

さらに、進学を希望していた理工科学校の受験にも失敗します。理由は、数学の理解をめぐって試験官たちと言い争ったことだといわれています。

なぜ自分の考え方は認められないのか。失意のガロアが数学研究の傍でのめりこむことになったのは、王政打倒の革命運動でした。地下活動やデモを繰り広げるガロアは、警察当局からも目を付けられ、やがて投獄されてしまいます。