「偏りのない真ん中の値」を計算する方法
今度は営業の仕事を例に、平均の歪みを見てみましょう。
住宅販売メーカーで営業を担当しているBさんは、住宅相談に来る人の平均年収が700万円であると計算しました。そこで、さっそく年収700万円の人に向けた新サービスを始めてみましたが、まったく手ごたえがありません。
その日相談に来た6人のお客さんの年収は、それぞれ300万円、400万円、400万円、900万円、1000万円、1200万円でしたが、一体なぜでしょうか?
6人の平均値を計算すると
300万円+400万円+400万円+900万円+1000万円+1200万円=4200万円
4200÷6=700万円
Bさんの計算通り、6人の平均年収は700万円になります。
しかし、実際に年収700万円の人は1人もいません。年収700万円の人に向けたサービスは、おそらく年収300万円~400万円の人にはやや高額に感じられるでしょう。一方、年収1000万円クラスの人にはあまり魅力的に映らないに違いありません。
つまり、どの顧客も新サービスのターゲット層に当てはまらないのです。
このように、少ないサンプルで計算した「平均」をビジネスプランのベースにしてしまうと、まったく効果のない施策になってしまうケースがあります。
世の中には平均値が溢れていますが、ビジネスパーソンなら平均値を見たときにまず、「その数字は偏っていないか」「サンプルの数は十分か」などを疑うべきです。
では、サンプル数が少なくとも、「偏りのない真ん中の値」を計算する方法はないのでしょうか。
そんなことはありません。「中央値」という数値を使えば、限られたサンプル数での「真ん中の値」を計算できます。
9人チームの中央値は上からも下からも5番目
中央値について理解するため、もう少し身近なケースを見ていきましょう。
昨今の働き方改革の影響を受けて、Cさんの会社でも「有休消化率50%」の目標が出されました。Cさんの部署は9人で、与えられる有給休暇日数は10日です。
目標を達成するには、1人あたり何日取得すればよいでしょうか。
答えは簡単で、1人あたり5日取得すれば50%に到達します。
しかし、現実では「その年の有給だけでなく、これまで累積してきた有給休暇をフルに使いきった人」もいる可能性も考えられます。
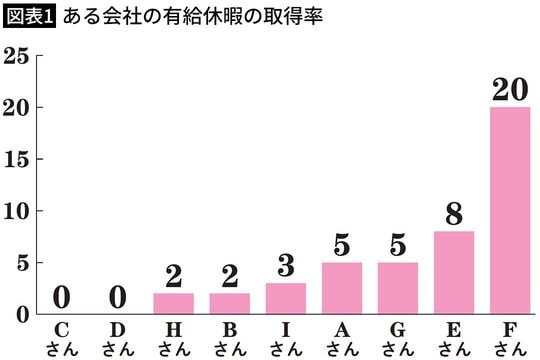
Aさん:5日
Bさん:2日
Cさん:0日
Dさん:0日
Eさん:8日
Fさん:20日
Gさん:5日
Hさん:2日
Iさん:3日
仮に、上記のような有給休暇取得率だったとしましょう。
平均有給休暇消化日数は5日です。先ほどの平均の歪みと同じですね。
このような状況で、実際の有給休暇取得率を計算したいときに役立つのが「中央値」です。
中央値とは、すべての人を並べたときに、真ん中に位置する人の数値を示すもの。このケースの場合は9人のチームですから、ちょうど「上からも下からも5番目」に当たる人を指します。よって、答えは「3」です。
有給休暇取得率30%なら、肌感覚に近い数値ではないでしょうか。