中でも藤ヶ谷太輔さんは年末ジャンボミニを購入し、4等1万円(当選確率0.3%)の当たりくじを333枚中6枚も当てていて、芸能人の引きの強さというか、強運ぶりに愕然とした視聴者も多かったと思います。
一方で、そんなに都合よく当たるわけが無い、やらせだったのではないかと言う人も一定数いたようです。そこで、藤ヶ谷さんの引きの強さが実際にはどれくらいの確率だったのか、「二項分布」と呼ばれる手法を用いて計算してみようと思います。
認識の歪みを検証する
「コインを投げて、表が出るか、裏が出るか」「宝くじを買って、当たりが出るか、外れが出るか」のように、起こる結果が2つしかない試み(試行)を「ベルヌーイ試行」と呼びます。
成功する確率をpとすると、失敗する確率は(1-p)と表せます。通常のコイントスは、1回やろうと、2回やろうと、成功する確率pは同じで、かつ1回目の試みが2回目の確率に影響を与えることはありません。
つまり何回目かによって成功する確率が変わったり、直前の結果が次に影響したりする状態は「ベルヌーイ試行」とは呼びません。そして今回の宝くじの場合は成功する確率pは同じで、1枚目の購入が2枚目の購入に影響を与えませんので「ベルヌーイ試行」が成立します。
このベルヌーイ試行をn回行って、成功する回数Xが従う確率分布を二項分布と呼びます。少し難しい話なので、順を追って説明します。
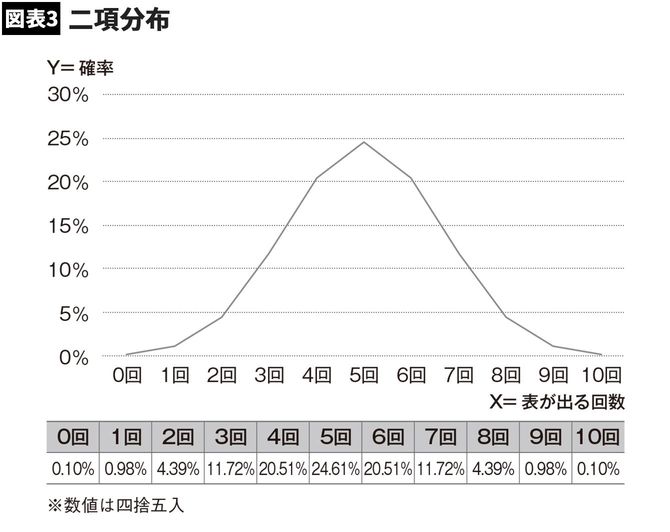
例えば、コイントス(表が出る確率が50%)を10回やったとして、何回表が出るでしょうか。表が0回のこともあれば、10回出ることもあると思いますが、大体4~6回くらいが多いでしょう。二項分布は0回しか表が出ない確率、10回表が出る確率、5回表が出る確率を表現してくれます。細かい計算式は省きますが、図表3のようになります。
表か裏かしか出ないなら、10回コイントスすれば半分の5回が多いのだろうと考えがちですが、実際は約25%しかその確率はありません。表が4回出る確率、6回出る確率はそれぞれ20%、足し合わせて66%です。
つまり10回のコイントスを3回行ったとして2回は「表が4回~6回出る」のですが、1回は「表が0回~3回、もしくは表が7回~10回出る」のです。50%の確率で表が出るのに、10回コイントスして1回も表が出なかったとしても、それは約0.1%の確率で起こる現象で、珍しいですがまったく起きないとは言い切れません。