「100回やれば当たるかもしれない」

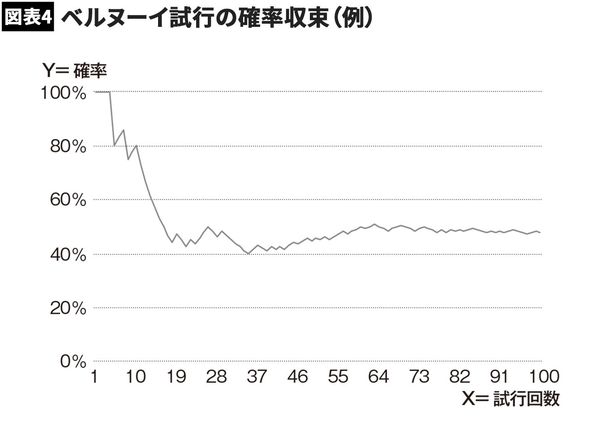
事象が起こる確率と、実際の結果には大きな乖離が生じるのです。最初は2回連続で表が出たり、4回連続で裏が出たりと、短期的に見れば以下の図のように「表が出る確率」は乱高下します。

しかし何十回と繰り返していくうちに、確率は少しずつ安定を見せ、やがて事象が起こる確率に収斂されていきます。冷静に考えればそうなのですが、なかなか納得できない人は多いでしょう。人間は確率に弱すぎるかもしれません。

【図表4】ベルヌーイ試行の確率収束（例）
『人は悪魔に熱狂する』

1％の確率でレアアイテムが当たるガチャがあったとします。100回課金してもレアアイテムが当たらない確率はどれくらいでしょうか。これも一種のベルヌーイ試行だと考えられます。ガチャを引くたびに確率が変わるわけではありませんし、1回目のガチャの結果が2回目のガチャの結果に影響を与えないという前提です。

「1％の確率で当たる」と考えるより、「99％の確率で外れる結果が100回連続起こる確率」だと置き換えて考えてみましょう。

正解は約37％です。思ったより高かったのではないでしょうか。よく考えてみれば「1％だとなかなか当たらない」と分かるのですが、直感で考えると「100回やれば当たるかもしれない」と感じてしまう。このズレが大きな「歪み」を生じさせるのです。

「運」に頼りすぎる人々

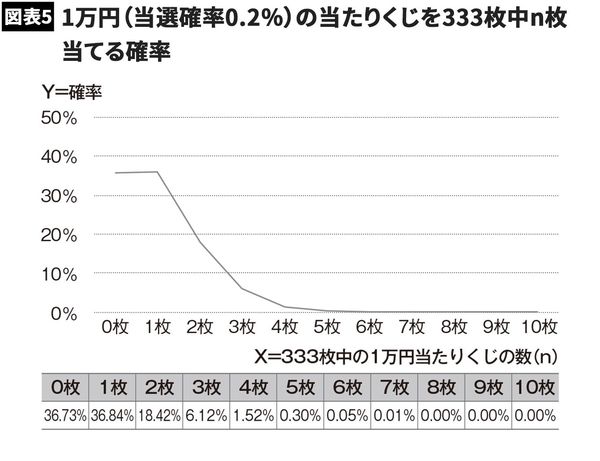
では、二項分布を用いて、藤ヶ谷太輔さんが4等1万円（当選確率0.3％）の当たりくじを333枚中6枚当てる確率はどのくらいか計算してみましょう。

当選確率は333分の1、0.3％です。外れる確率は99.7％なので、まずは外れが333回連続で起こる確率を考えてみましょう。

正解は約37％です。逆に言えば1枚以上当たる確率は約63％あります。細かい確率は図表4の通りです。ちなみに図では省略していますが、333回中10枚以上当たる確率は0.00001％と非常に低い確率です。

米国国家安全運輸委員会の調べでは全世界の航空会社の総合平均値で見た、乗った飛行機が墜落する確率は0.0009％だそうですから、10枚当てるのは飛行機が墜落するよりもさらに低い確率ということになります。

【図表5】1万円（当選確率0.2％）の当たりくじを333枚中n枚当てる確率
『人は悪魔に熱狂する』

藤ヶ谷さんは333回中6枚当てたのですが、その確率は約0.05％、約10000回に5回です。そんな低い確率を引き当てるなんて普通ありえないじゃないか、ヤラセじゃないか、と思われるかもしれませんが、確率が低いだけでは「起きない」と言い切れません。滅多に起きない事象であったとしても、起こる可能性はゼロではないのです。