なぜ、算数や数学には平易な言葉なのにややこしい出題が多いのか。AI研究者の新井紀子さんは「生活言語ではふつう、『いくつかの』は2つから6つくらいまでの少ない複数を意味しますが、数学では異なる意味を持っている」という――。

※本稿は、新井紀子『シン読解力　学力と人生を決めるもうひとつの読み方』（東洋経済新報社）の一部を再編集したものです。

摩訶不思議な「数学語」の世界

小学校高学年から高校入学までのどこかで、「どんなに努力しても数学だけはダメだから、絶対に文系に行くしかない」と固く思い込んでしまう人は少なくありません。私もそのひとりでした。高校を卒業するまで一番嫌いな教科は数学でした。消去法で一橋大学の法学部に進学しました。

成績はそこそこよかった、国語の成績は文句なかった、本もたくさん読んだ、意欲関心もあるのに、数学（と体育）はダメ、という状態でした。タイムスリップできたなら、数学ができないことに悩んでいる高校生の私に、「あなたは数学が苦手なわけじゃない。国語の力で無理に数学を読もうとして失敗しているだけよ」と言ってやりたいですが、たぶん、高校生の私は耳を貸そうとしないでしょう。

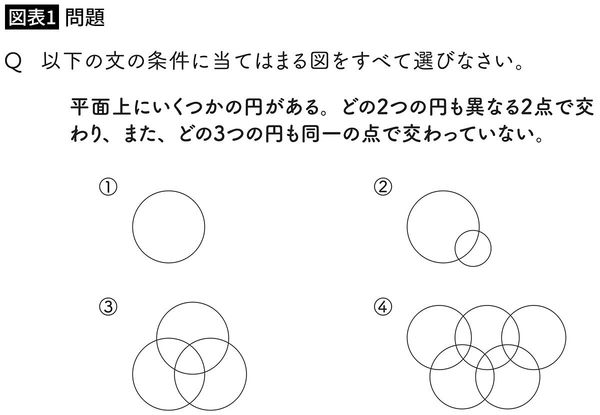
その「高校生の私」に見せたいものがあります。次の問題です（図表1）。

問題文に出てくる数学用語らしきものは「平面」、「円」、「交わる」くらい。どれも難しい用語ではありません。

【図表1】問題　以下の文の条件に当てはまる図をすべて選びなさい。平面上にいくつかの円がある。どの2つの円も異なる2点で交わり、また、どの3つの円も同一の点で交わっていない。
出典＝『シン読解力　学力と人生を決めるもうひとつの読み方』（東洋経済新報社）
全ての画像を見る（3枚）

この文には3つの条件が書かれています。

1．平面上にいくつかの円がある。
2．どの2つの円も異なる2点で交わっている。
3．どの3つの円も同一の点で交わっていない。

この3つの条件をすべて満たすものを選ぶ、という問題です。

ヒントを差し上げます。条件を満たさない図はひとつだけです。

高校生の私は、迷わず選択肢①の、円がひとつだけの図を除外するでしょう。なぜなら円がひとつしかないのですから、条件2の「どの2つの円……」、条件3の「どの3つの円……」を満たすわけがないからです。みなさんもそうお答えになるのではないでしょうか。

ところが、これが不正解なのです。

「中学受験＆探究編〜プレジデントFamily祭2025」申込受付中！ 
日時：2025年9月28日（日） 10:00 ～ 16:00
会場：東京・神田明神ホール
チケット：1,500円（税込／軽食付き／先着順／事前申込制）

 

「中学受験」と「探究学習」についての理解を深め、子供たちの将来の可能性を広げるための選択肢を紹介するイベントを開催します。「声の教育社」代表・後藤和浩さん、聖光学院校長・工藤誠一さん、動物言語学者・鈴木俊貴さんなどをお招きし、中学受験の最新情報や自ら学ぶ子の育て方、今の時代の子供に本当に必要な力などをセミナー形式でお伝えします。

詳細＆申込はこちら