「都合が良いこと」は本当に正しいのか

この先の目標は、この“都合が良いこと”が本当に正しいのかを確かめることです。

ケンプは次のことに着目します。

どんな国にも「二辺国」「三辺国」「四辺国」「五辺国」と呼ばれる国のいずれか1つは必ず含まれる。

次のように、二カ国に接している国を「二辺国」、三カ国に接している国を「三辺国」、四カ国に接している国を「四辺国」、五カ国に接している国を「五辺国」と呼びます（図表8）。

出所＝『笑わない数学』

ケンプが着目した事実を、まだ4色で塗り分けOKとわかっていないn＋1カ国の箱に当てはめてみると、箱の中の地図たちは「二辺国」を含む地図、「三辺国」を含む地図、「四辺国」を含む地図、「五辺国」を含む地図の4つに分類できるのです。

出所＝『笑わない数学』

ここからは、箱の中で4つに分類された地図がそれぞれ4色で塗り分けられるか考えていきます。

ケンプの「天才的な発想」

まず、二辺国を含む地図について考えていきましょう。

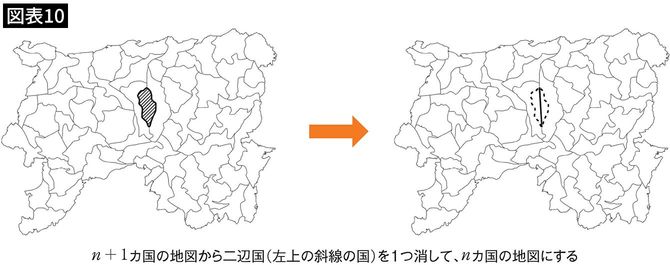
ここで、ケンプは二辺国を消して考えてみるということを思いつきました（図表10）。

出所＝『笑わない数学』

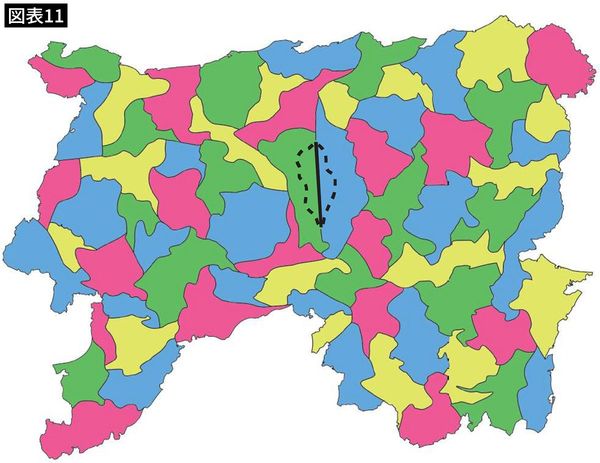
二辺国を消したこの地図の国の数は1カ国減りnカ国の地図になりました。nカ国の地図は、すべて4色で塗り分けできると仮定しているので、このnカ国の地図は4色で塗ることができます（図表11）。

出所＝『笑わない数学』

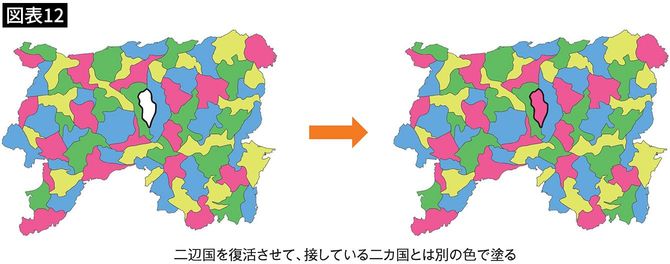
ここで、先ほど消してしまった二辺国を復活させます。

すると、二辺国は接している二カ国とは別の色で塗ることができますので、地図全体を4色で塗り分けられたということになります（図表12）。

出所＝『笑わない数学』

つまり、二辺国をひとつでも含むn＋1カ国の地図は、すべてこの方法で塗り分けOKだと証明できたことになります。

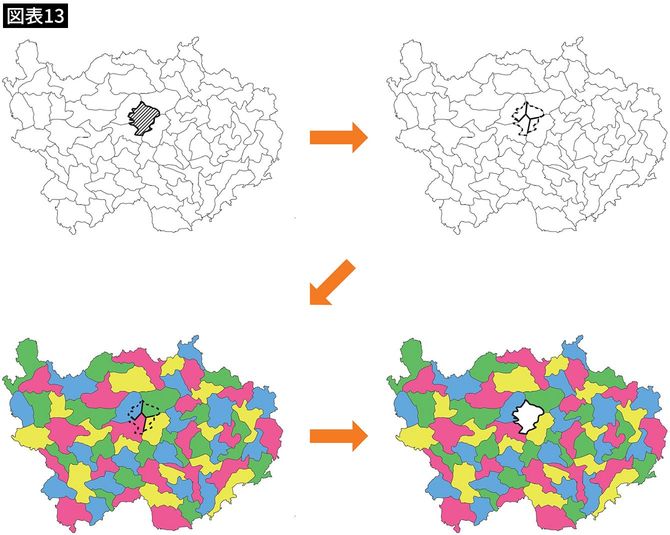
三辺国を含む地図、四辺国を含む地図も、同じように、1カ国減らして4色で塗り分けし、国を復活させて色を塗るという方法で塗り分けOKだと証明できます（図表13）。

（実は、四辺国を含む地図は単純にはいかないのですが、ケンプの天才的な発想で証明できます。）

出所＝『笑わない数学』