男女2人ずつでのマッチングを考える

誰が誰を好きになるかということ以外に考慮すべきことがなければ、ただ好きな人同士をマッチングさせればいい、と考えることもできますね。つねにそのように簡単な例から探求が始まります。

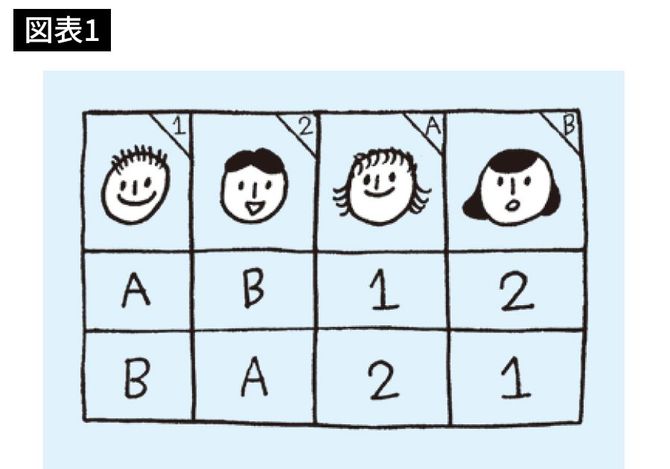
投票問題と同じように、基本的な情報は選好度表にまとめればいいでしょう。男性は女性たちを、女性は男性たちを選好度の順に並べて、仲人である私たちに提出させます。最も単純な、男女が各2人という状況であれば4通りの選好度表ができます。

イラスト＝『教養としての数学』
『教養としての数学』より

表の読み方はわかりますか？

男性1は女性Bより女性Aの方が好きであり、男性2は女性Aより女性Bの方が好き。このように読みます。では、どうマッチングすればいいでしょうか？

このケースはシンプルです。{男性1、女性A｝{男性2、女性B｝。このようにマッチングさせればいいでしょう。先に言ったように、ただ好きな相手同士をマッチングさせればいいと思います。

功利主義では「よいマッチング」を考えることはできない

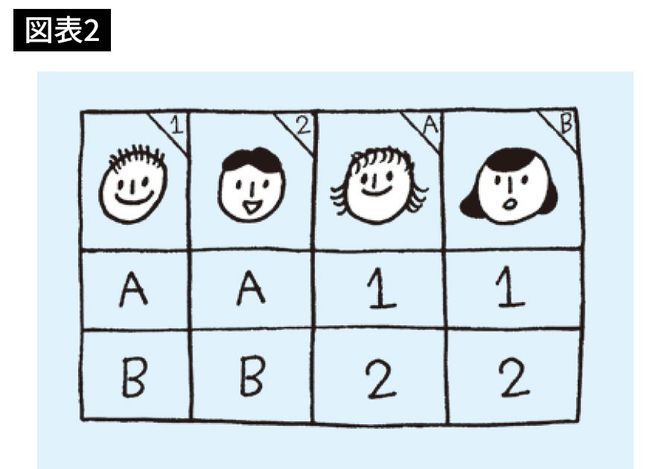
ところが問題は、現実にはこんな単純な選好度表はめったにできないという点です。普通はどんな現象が起こりますか？　図表2のようなケースの方が多そうです。

イラスト＝『教養としての数学』
『教養としての数学』より

これはモテる男性とモテる女性がいる状況です。男女が2人ずつしかいなくても、こうしたケースはよくあります。今度はどうすればいいでしょうか？

可能性は2つしかありません。｛男性1、女性A｝{男性2、女性B｝とするか、｛男性1、女性B｝｛男性2、女性A｝とするかのどちらかです。

では、この2種類のうち、どちらの方がよいマッチングでしょうか？

もっと情報がないとわからないと思いますが、情報はこれだけとしましょう。

まず、｛1、B｝｛2、A｝について考えてみましょう。そうすれば各カップルに1人ずつは幸せになれますから。功利主義的な観点が示されましたね。

ですが、不幸にも功利主義では問題は解決しません。なぜなら｛1、A｝｛2、B｝としても幸せな人は2人、｛1、B｝｛2、A｝としても幸せな人は2人になりますから。満足する個人の数から見ても、2つの方法は同等に思われます。

でも、満足するカップルが多いことを基準にすれば、最初の場合の方がよりよい方法です。満足するカップルが生まれることがより重要だということ。それは非常に重要な指摘です。そのアイディアを足掛かりに、もう少し体系的に考えてみましょう。