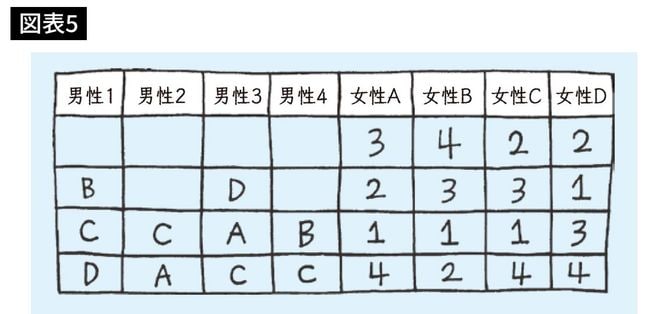
魅力的な女性1人を2人の男性が奪い合うと、どうなるか
第3ラウンドで男性4は選好度3位の女性Bにプロポーズする番です。
では、どんなことが起きるでしょうか? それこそ恋愛小説のような構図ですね。
女性Bはすでに第1ラウンドで男性3と婚約していますが、もともとの選好度1位は男性4でした。婚約を破棄してもいいなら、女性Bは男性3との婚約を破棄して、もっと好きな男性4のプロポーズを受け入れるでしょう。
そうなると、男性3は再びラウンドに出て、選好度2位の女性Dにプロポーズすることになりますね。では、どんな問題が起きるでしょうか?
女性Dは、男性3よりも現在の婚約相手である男性2の方が好きですから、男性3からのプロポーズを断るでしょう。すると次にはこんな状況が起こります。
男性3は選好度3位の女性Aにプロポーズします。女性Aは現在の婚約者の男性1より男性3の方が好きなので、男性1との婚約を破棄して、男性3と婚約することになります。
ラウンド4が終わった段階で、成立しているカップルは{2、D}{3、A}{4、B}となります。そうすると、男性1がまたプロポーズをしなくてはなりません。
第1ラウンドで婚約した女性Aを男性3に奪われた男性1は、今度は選好度2位の女性Bにプロポーズします。ですが、女性Bは現在の婚約者の男性4と男性1を比べて、選好度が上位にある婚約者4との婚約を維持することを選びます。
挫折した男性1は、今度は女性Cにプロポーズします。いま相手のいない女性Cは、男性1のプロポーズを受け入れることになります。
最終的な組み合わせは{1、C}{2、D}{3、A}{4、B}となります。こうしてアルゴリズムは完結します。あとは結婚するだけです。選好度表をあらためて見直しながら、浮気する可能性を調べてみるとどうなるでしょうか。
たとえば、男性1はいまの相手より女性A、Bの方が好きですが、女性Aは自分の選好度1位の男性3と結ばれており、女性Bも第1位の男性4と婚約しているので、2人とも男性1 を受け入れる必要がありません。したがって、男性1にはもはやチャンスはありません。
完璧に見えるアルゴリズムだが…
私たちが本当に結婚仲介業者で、男女のお互いの選好度情報を持っていれば、互いにお見合いをさせて時間を浪費する必要もありません。単にこのアルゴリズムのとおりにカップルをつくればいいだけだからです。
このアルゴリズムを作ったのは、デビッド・ゲールとロイド・シャプレーという二人の数学者です。1962年に発表した論文「大学入学と結婚の安定性」で紹介しています。
二人の名を取ってつけられた「ゲール=シャプレー・アルゴリズム」は、答えがあるというだけでなく、答えを効率的に求める方法まで提示しています。これを使えば、男女の役割を取り換えることもできるし、答えが複数あればその中からどれを選択するかも考えることができます。シャプレーはこの理論によって2012年にノーベル経済学賞を受賞しました。
ただ、1つ疑問が浮かびます。
ゲール=シャプレー・アルゴリズムでは、プロポーズできるのは男性だけとなっています。女性が先に選択できないのは、何となく女性に不利に思えますが、はたしてこのアルゴリズムは女性と男性、どちらに有利なんでしょうか?