ノーベル賞の数学理論の結論…｢理想の結婚相手｣に最短で出会うためにやるべきこと ｢好きなら先に告白せよ｣

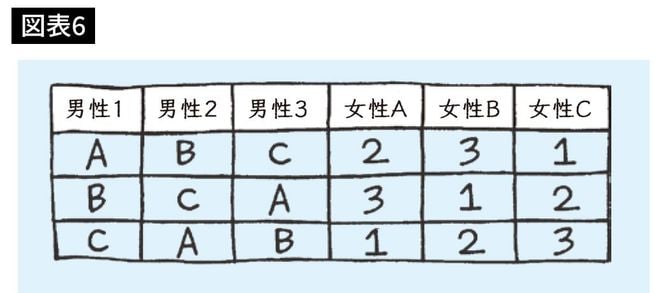
女性は「最も嫌いな男性」とマッチする

私たちが使ったアルゴリズムは、確実に男性にとって有利です。

図に示す例で少し調べてみましょう。

『教養としての数学』より

この表のようなケースをゲール＝シャプレー・アルゴリズムで考えてみると、第1ラウンドで男性1は女性Aに、男性2は女性Bに、男性3は女性Cにプロポーズしますね？　その次に、アルゴリズムはどうなりますか？

女性は自分にプロポーズした人の中から気に入った相手を受け入れます。ところが、女性がそれぞれプロポーズを1回しか受けられないので、第1ラウンドで男性1と女性A、男性2と女性B、男性3と女性Cがそれぞれ婚約することになります。

次の段階は第1ラウンドで選ばれず婚約していない男女が第2ラウンドでマッチングすることになりますが、第2ラウンドは行われずに終わります。｛1、A｝｛2、B｝｛3、C｝というカップルが成立して、結婚することになりますから。

このように見ると、女性たちは自分が最も嫌いな男性がプロポーズしてきても、このアルゴリズムにしたがってそのまま結婚しなくてはなりません。

一方、男性たちは自分がいちばん好きな女性と結婚することになります。男性たちが全員満足したため、他の女性を探す必要がないというわけですね。安定したマッチングではありますが……。

アルゴリズムの教訓は「好きなら先に告白せよ」

ゲール＝シャプレー・アルゴリズムにおいて男性は自分にとってマッチング可能な女性のうち、選好度が最も高い女性と結婚することになります。

キム・ミニョン『教養としての数学　数学がわからない僕と数学者の対話』（プレジデント社）

そして、最終的に結ばれた女性よりも選好度が高い女性と結ばれようとすると、どこかに不安定性が生じます。

一方、女性はマッチング可能な男性のうち最も選好度が低い男性と結婚することになります。この現象を上の例がよく示しています。

こうして見ると、男性に圧倒的に有利な仕組みと言っていいでしょう。

私はある講義で、このアルゴリズムの教訓は「好きなら先に告白せよ」ということだと言いました。

もし振られたとしても、自分の選好度の順に告白する方がよい結果が得られるのですからね。男性の場合を考えると、選好度の低い女性とカップルになったとしても、すでにそれより選好度の高い女性からは振られた状態ですから、婚約破棄の原因はなくなっているわけです。