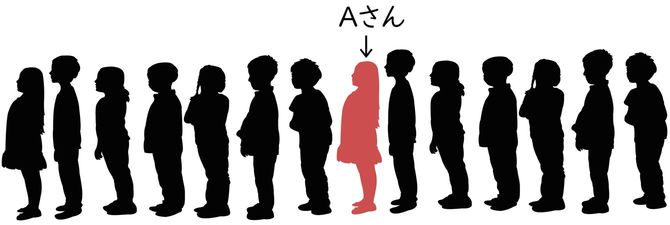
誤答率7割「1列14人でAの前に7人。後ろに何人？」
例題1
子どもが14人、1れつにならんでいます。
ことねさんの前に7人います。
ことねさんの後ろには、何人いますか。
▼誤答例
式 14−7＝7
答え 7人
▼正解（3年生の正答率 28.1％）
式 14−7−1＝6
答え 6人
「問題文にある数字を使えば解ける」という思い込み
この「列の並び順問題」は小学1年生の教科書で習うものですが、算数教師の間でも、子供がつまずきやすい問題として有名です。
間違える子の多くが7人と答えますが、それには理由があるのです。
間違える原因の一つ目は、問題文を正しく読まず（あるいは読むことができずに）出てくる数字を使って思いついた計算をしてしまっているということ。
前ページで説明したように、子供は、それまでの経験から素朴な思い込み＝スキーマを持っています。この間違いをする子は、たとえば次のようなスキーマを持っていることが考えられます。
「問題文に出てくる数字で計算すれば文章題は解けるはずだ」
「答えが小さくなりそうなときはひき算をすればいい」
その思い込みのルールの通りに、14－7＝7と計算してしまうのです。
それでも、見直しをすればあるいは間違いに気がついたかもしれませんが、自分の答えを客観的に見るためのメタ認知能力（文末参照）が十分に育っていないのでしょう。
正解するためには、「全体の14人から前にいる7人を引いた数には、ことねさんが含まれるので、さらに1人を引く」と筋道を追って類推する必要があります。問題文にはない「1」という数字を導き出して計算することが必要ですが、それはとても高度なことなのです。
「前」「後ろ」という言葉が身についていない
この問題が難しいもう一つの理由は、多くの子は、「前」「後ろ」という言葉が生きた知識になっていないことです。
この例題では、全部で14人いる→ことねさんの「前」に7人いる→ことねさん（1人）がいる→ことねさんより「後ろ」には何人いるか
という関係がイメージできなくてはなりません。
日常生活のなかでも、前・後ろ、右・左などの言葉を多く使うことが、生きた知識とするために有効です。そのときに「誰の右かな」「どっちが前かな」などと方向や基準点を意識させるようにするのもいいでしょう。
（後編では、間違いやすい文章題その2、3を紹介します。関連記事：後編 小6の43％が誤答｢8人に4Lのジュースを等しく分けると1人何リットル?｣迷いなく8÷4と立式する子への教え方）