偏差値で重要なのは、全体における自分の位置

私たちが受験期に使っていた偏差値は、標準偏差の応用です。簡単に言えば、全体の中で「自分がどのあたりに位置しているか」をよりわかりやすく数値化したものになります。

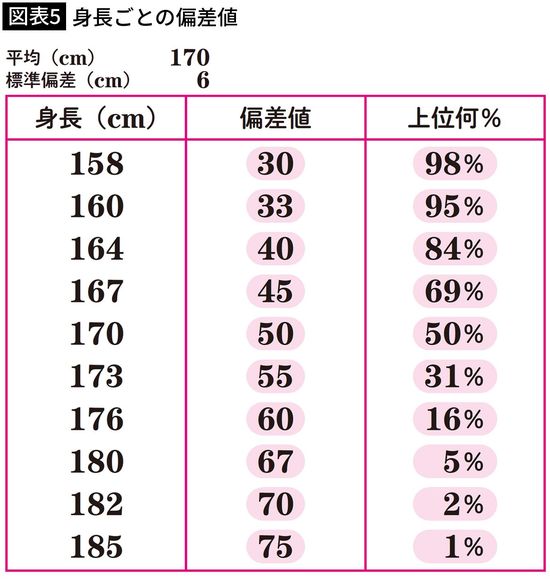
平均身長170cmの例を使って、偏差値を出してみましょう。

まずは平均値を「偏差値50」と定め、標準偏差1つ分を10として扱います。この場合は平均身長170cmが偏差値50、標準偏差6cm分が10です。

たとえば身長176cmの男性は、

偏差値50（170cm）＋偏差値10（6cm）＝偏差値60

と計算できます。

身長164cmなら、

偏差値50（170cm）－偏差値10（6cm）＝偏差値40

となるのです。

ただ、この偏差値40や偏差値60といった数字は、単なる計算結果でしかありません。偏差値で重要なのは、全体における自分の位置を考えることです。

図表5を見てみましょう。これは先ほどの身長ごとの偏差値をまとめたものです。

それぞれの偏差値の横に「上位何％」という数字が書かれていますが、意識すべきはこの数字です。

たとえば偏差値60ということは、上位16％に位置しているという意味。100人いたら上から16番目になる、ということです。

偏差値40なら上位84％。100人中84番目になります。

受験で偏差値が使われていたのは、この「上位何％」という考え方が重要だったからです。

【図表5】身長ごとの偏差値
出所＝『頭のいい人が使っているずるい計算力』

「みんな」は標準偏差で人数がわかる

さて、先の記事でも問いかけ続けてきた問題に戻りましょう。「みんな」とは、一体誰を指すのでしょうか？

正規分布の考え方からすれば、みんなとは「真ん中の68％の人」というのが答えになります。極端な2％の人の意見は、「みんな」とは言えません。全体の16％の人の意見も、「みんな」と言うには無理があるでしょう。

つまり、冒頭の会話であった「取引先はみんなあんまり乗り気じゃなさそう」という意見も、正確には「約68％の取引先はあんまり乗り気じゃなさそう」と言うべきなのです。支持する取引先も16％はいる、ということになります。

取引先から一切支持されない施策と一部支持の施策では、改善案の方向性も変わってくるはずです。このように、正規分布で正しい数値を確認することは、現状を正しく把握することにつながります。

また、ちまたには「2：6：2の法則」というものがあり、社内で何か新しいことを始める場合、最初は「中立が68％、支持が16％、反対が16％」くらいになることが多い、とされています。その中に、極端な支持と不支持がそれぞれ2％ずついるというわけです。

斎藤広達『頭のいい人が使っているずるい計算力』（PHP研究所）
斎藤広達『頭のいい人が使っているずるい計算力』（PHP研究所）

実際に自分が所属する会社で考えてみるとどうでしょうか。

あくまで経験則から生まれた数字のようですが、それほど的外れな数字ではないように思えます。

それに、2：6：2の法則、あるいは正規分布と標準偏差の考え方を仕事に取り入れることで、さまざまなメリットがあります。

たとえば、一部の極端な意見に対し「2％は絶対にそういう人が現れる」と思えば、うまくスルーすることもできるでしょう。