富裕層がお金が増えてもあまりうれしくない理由
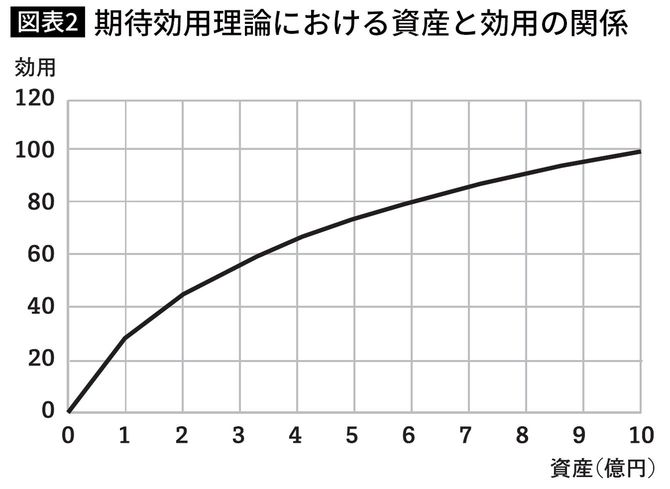
効用というのは心の中の動きですので、単位はありません。嬉しいと感じるときには、数字が大きくなるというように考えてください。図表1をグラフにしてみると、次のようになります(図表2)。
ベルヌーイの想定では、資産が増えるとともに効用も増えていきますが、その増え方がだんだん小さくなっていくことがわかります。これはどうしてそうなのでしょうか? どなたかいかがでしょうか?
【B】資産がゼロから1億円になるのはすごく嬉しいですが、資産が増えていくと、さらに1億円増えることによる嬉しさの度合いがだんだん小さくなっていくということだと思います。
【岩澤】おっしゃるとおりですね。このようなグラフを「上に凸型」といいます(※3)。ベルヌーイは資産と効用との間には「上に凸型」の関係がある、と主張したわけです。そして実は、そこにはもうひとつ深い意味がありました。それはこの「上に凸型」の関係が、人々のリスク回避の性向をうまく示しているということでした。
※3 数学的には「凹関数(concave function)」または「上に凸関数」と呼ばれる。
「50%の確率で10億円」なのに、「100%5億円」を選ぶ
たとえば、「今すぐ5億円あげます」という選択肢と、「50%の確率で10億円、50%の確率で0円」という選択肢を比べると、多くの人は前者を選びます。ここで上の表とグラフの数字を当てはめて考えてみましょう。
「今すぐ5億円」ということだと、その効用は74です。一方、「50%の確率で10億円、50%の確率で0円」はどうでしょう。効用で考えると「50%の確率で100、50%の確率で0」ですから、効用の期待値——「期待効用」と呼びます——は0.5×100+0.5×0=50です。
効用が大きいのは「今すぐ5億円」のほうなので、このような「上に凸型」の効用を持っている人は「今すぐ5億円」を選ぶはずだと議論できるわけです。人々は不確実な将来について選択する場合に、その選択肢のもたらす収益の期待値ではなく、期待効用に基づいて選択する。そして人々の効用は、資産に対して「上に凸型」、つまりリスク回避型の特徴を持っている。このような考え方を「期待効用理論」といいます。
※4 数学的には「凹関数(concave function)」または「上に凸関数」と呼ばれる。