小遣い｢1年目は5000円で年1000円ずつ増｣｢半年で2500円､半年ごと250円増｣どっちが得か…答えに大人も愕然 2cm×100.5cmの長方形の箱に直径1cmの乾電池が201本入る謎

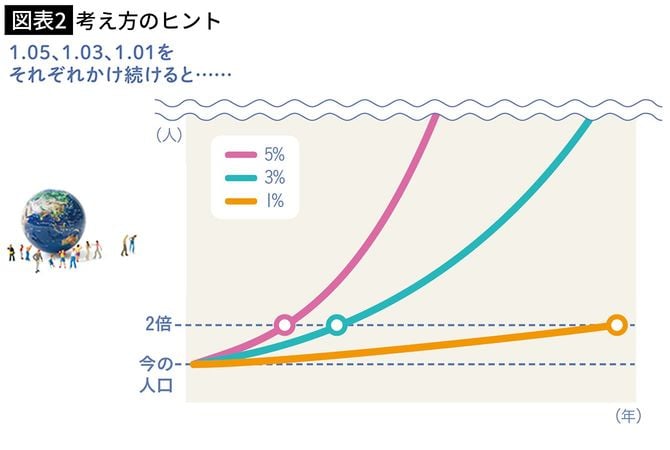
Q5　A国、B国、C国があります。1年間に増える人口を調べたところ、A国は1％、B国は3％、C国は5％でした。毎年同じ割合で増えるとすると、人口が倍になるのは、それぞれ何年後でしょう？

A　この問題は、電卓で同じ数に1.01、1.03、1.05をそれぞれかけ続けて最初の数の倍になる数を数えていってもいいのですが、資産運用で元本を2倍に増やすときの、おおよその金利や年数を簡単に導き出す「72の法則」にあてはめれば、あっという間に答えが出ます。

撮影（物）＝市来朋久

出所＝『プレジデントFamily 算数が大得意になる 2023完全保存版』

「72の法則」の計算式は、「72÷金利（％）＝年数（年）」。ここでいう金利は、年1回・複利計算です。今の日本ではありえない数字でうらやましい限りですが、たとえば銀行に年利7.2％で預けておけば、10年で元本の倍になる。

72の法則はあくまで概算なので、実際の年数とは少し違ったり、金利によって誤差があるなどの問題もありますが、72という数字は覚えておいて損はありません。

問題は、金利ではなく各国の人口の増え方を求めるものですが、この計算式にあてはめて考えると、A国は約72年（72÷1）、B国は約24年（72÷3）、C国は約14年（72÷5）でもとの人口の倍になるということがわかります。

『プレジデントFamily 算数が大得意になる 2023完全保存版』（プレジデントムック）

複利という点がポイントで、わずか数パーセントの違いなのに、年数には大きな開きが生じます。もしもこれが人口ではなくお金、しかも借りる場合だったら要注意ですよ。

というのも、72の法則を使えば、借金をして、まったく返済しないでいたら、何年で金額が倍になるかというような恐ろしい計算も瞬時にできます。たとえば200万円を借りたときには、金利15％だとわずか4.8年、金利20％だとさらに早く3.6年で倍の400万円になってしまう。

この数字を見たら、私は怖くてとてもじゃないけれど借金などできません。自分の身を守るためにも、やはりきちんと計算することが重要ですね。（答え　A国＝約72年、B国＝約24年、C国＝約14年）