想像ベースの議論は先入観に導かれている可能性がある

店舗の規模以外にも間に入りそうな要素を挙げることはできますが、あくまで思考過程の例を見るのがここでの目的ですので先に進みます。

ミッシングリンクを埋める直接的要因の候補が見つかり、自信があるのならそのままこれを反論として主張してもよいでしょう。住民が見栄っ張りだから人口当たりの美容院の数が多いのではなく、美容院の規模が小さいから数が多くなるのだ、というように。

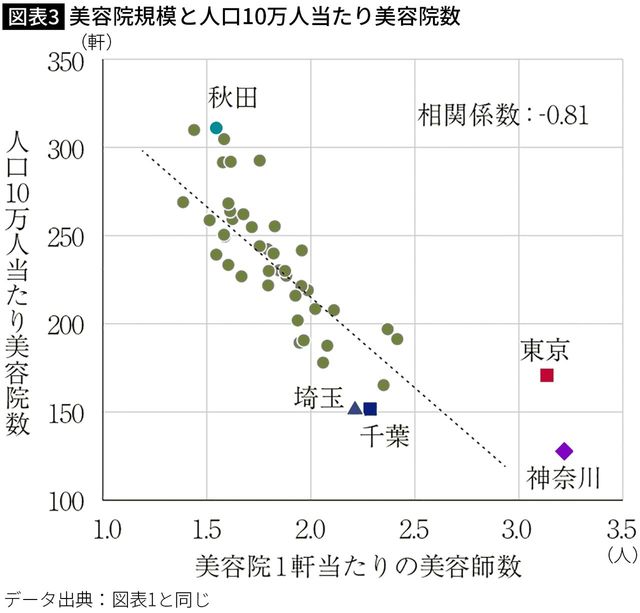
ただし、想像を基にした議論は、先入観に導かれている可能性が常にあります。そこで、自分の説をより確かなものにするために、相手説と同じ数字を観察するだけでなく簡単に分析をしてみます。ここでは、基本的な分析の手法である散布図を作成し、相関関係（後述）の様子を確認してみます。これにより、店舗規模が実際に10万人当たり美容院数の要因となっていそうか考察することができます。店舗の規模の指標としては美容院1軒当たりの美容師数を採用します。

【図表3】美容院規模と人口10万人当たり美容院数
出典＝『データ分析読解の技術』

図表3は、美容院1軒当たり美容師数と10万人当たり美容院数との関係を見た散布図です。散布図とは、たとえば体重と身長のように、ひとつのセットとなった2つの数字を、それぞれの数字に応じて縦軸と横軸の決まった位置に印を置くことを繰り返して作られるものです。この縦軸のことをy軸、横軸のことをx軸と呼びますが、わかりにくいのでここでは縦軸、横軸で通します。

大事なことをひとつだけ伝えておきます。散布図は縦軸が結果、横軸が要因となるように描きます。これは原則で、因果関係を意識しないで傾向を観察するときや、特別な意図がある場合は別です。なので、特に意図がなさそうなのに結果が横軸、要因が縦軸となっている散布図が出てきたら、怪しい分析ではないかと警戒することができます。ここでは人口10万人当たり美容院数を結果として、1軒当たりの美容師数を要因として意識して散布図を描いています。

相関関係と因果関係の違い

この散布図において①一方の数値が大きい場合に他方も同様に大きくなる傾向、あるいは②一方の数値が大きい場合に他方が小さくなる傾向が明確なことを「相関している」、「相関関係にある」と表現します。また、①を正の相関関係、②を負の相関関係と呼びます。この正・負の相関関係を確認する、示すために散布図は作成されるものだと言ってよいでしょう。

なお、散布図で示されるような連続的な関係だけでなく、2つのグループの間の傾向の違いも相関関係と表現します。たとえば、男性よりも女性のほうが新型コロナウイルス・ワクチンの副反応を報告する割合が高いというのも、性別と副反応の相関関係です。この場合、相関関係に正も負もありません。

また、厳密には散布図の点の分布がU字型や他の形の場合でも、2つの数値の関係が明確であれば相関関係と呼びますが、ここでは取り扱いません。一般にも、2つの要素の単調な増減同士の関係（線形関係）を相関関係と呼ぶことが多いと思います。図表3に付した相関係数は、この要素同士の線形の相関関係の強さを指標化したものです。

ここで注意しておきたいのは、相関関係と因果関係とは異なるものということです。相関関係は、ある数値の大小が他の数値の大小または小大と関連する傾向にあることを示す言葉です。一方が先に動き他方がこれに応じて動く、要素間の先後という因果関係の性質を相関関係は含みません。一方が他方を動かしていることを明らかにするものでもありません。

散布図は相関関係を示してくれますが、それが因果関係かどうかの判断は散布図ではできません。散布図は因果関係を意識して描きますが、これでわかるのは相関関係でしかないのです。