紙ナプキンは必需品!
この本の原書『Drawing Physics』のカバーを見てにやりとしました。コップの跡がついた紙ナプキンの上に、ピロポノスの自然落下のスケッチが描かれています。これはまさにわれわれ物理学者がよくやること。喫茶店やレストランで集まると、ああじゃないかこうじゃないかと描き始めるんです。ギリシャ時代には紙ナプキンはありませんでしたが、何か身の回りにある絵に描ける概念を使って考えるという営みは、タレスやアリストテレスの時代から変わっていないのです。
物理学者は最終的には法則を数学の言葉にするわけですが、そこに行く前にこういうことはいつもやっているんです。目に見えないX線や物質波、ニュートリノやヒッグス粒子などが実際に存在するのか、その振る舞いにはどんな法則が当てはまるのか、といったこともまずは描いて考える。
実際は、絵を描きながら常に数式を頭に思い浮かべています。たとえば、ヤングの2重スリット(第32章)の絵は、三角関数の足し算ですね。また、ド・ブロイの物質波(第45章)の絵は波動方程式を表しています。電子の持つ波の性質を表すものですが、バイオリンの弦の振動を表す数式もこれと同じです。ひとつの考え方や式がいろんなものに当てはまるというところが物理学の醍醐味でもあります。
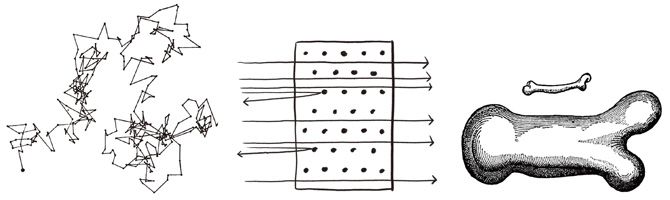
ほかにも光電効果(第38章)、ブラウン運動(第39章)、ラザフォードの金箔実験(第40章)ヒッグス粒子(第51章)などは、この絵を描かずしては物理の授業にならないというくらい定番の絵が紹介されています。それからちょっと変わったところでは、ガリレオが描いたという大小2本の骨の絵が出てきますね(第22章)。この絵が表しているスケーリングという考えは、非常に重要で、宇宙の話にも物質の話にも素粒子の話にも出てきます。
金属に電気を流す場合、3次元空間だといくら大きなものでも問題ないのですが、たとえば金属板のような2次元のものだと、大きくしていくとどこかで電気が流れなくなる。何かをどんどん大きくしていくとその性質がどう変化するかというのも数式で表せます。この場合は微分です。ただ、時代が下って現代に近づくにつれて、新しい理論を単純な絵で描くのはなかなか難しくなります。そういう理由でアインシュタインの特殊相対性理論なども入っていないのでしょう。