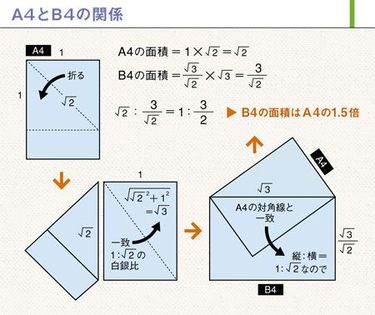
まず、A4を縦にして図のように上の正方形の部分を斜めに半分に折る。この正方形の一辺と対角線の比は白銀比(1対√2)。そして、この対角線とA4の縦の長さを比べると一致する。つまりA4の横の長さを「1」とすると、縦は「√2」ということになる。
ここで中学で習う「三平方の定理」(直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると「aの2乗+bの2乗=cの2乗」)を使い、A4の対角線の長さは「√3」とわかる。
次に、A4の対角線とB4の縦の辺を重ねてみる。するとぴったり一致する。つまりB4の縦の辺は「√3」ということになる。すると前述したようにコピー用紙はすべて白銀比なので、B4の横の長さは「√2分の√3」となる。
最後に、これまで割り出された数値を使ってA4とB4の面積を求めてみよう。A4は「√2×1=√2」、B4は「√3×√2分の√3=√2分の3」。したがって、A4とB4の面積比は、「√2対√2分の3」で、B4の面積はA4の面積の1.5倍とわかるのだ。
最後に0判同士で検証してみよう。A0判は「1189mm×841mm」でその面積は999949平方ミリメートルで約1平方メートルとなる。一方、JISでB0判は「1030mm×1456mm」と定められていて、その面積は1499680平方ミリメートルで約1.5平方メートルである。普段、何げなく手にしているコピー用紙だが、その根底にある数と形の仕組みで、私たちは便利に使えるのだ。