世界地図の国別色分けが4色で十分な理由

欧州では歴史的に何度も国境線が引き直された。そのたびに地図を書き直さなければならず、それはとても重要な仕事だった。複雑に絡まる国境線だが、当時の印刷職人は、隣接する2つの国を違った色に塗り分けるとき、平面上のどんな地図も最大4色あれば塗り分けられることを経験的に知っていたといわれる。

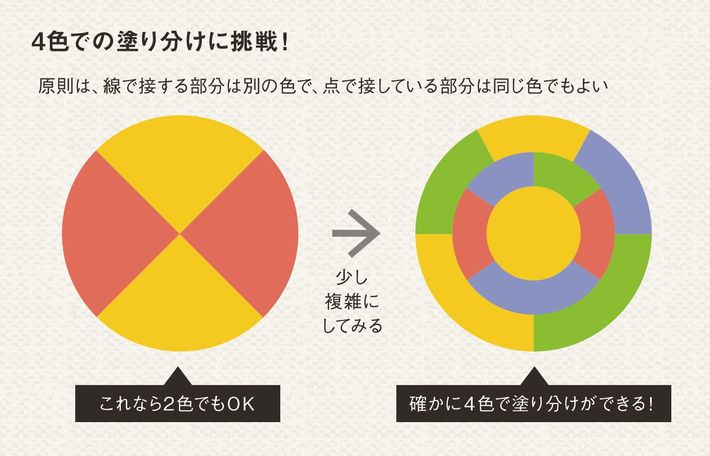
そう聞くと、何十、何百という区分けを本当にたった4色で塗り分けられるのか不思議に感じるかもしれない。まず、塗り分けの原則として、左の図にあるように、線で接する部分は別々の色にし、点で接している場合は同じ色でもよい。そして、これを踏まえた複雑な図形の塗り分けの例が右の図で、確かに4色で塗り分けられている。

全ての画像を見る（1枚）

このように平面上のどんな図形も4色で塗り分けられることを「四色定理」という。1852年、英国のフレデリック・ガスリーが初めて問題提起し、多くの数学者が4色で塗り分けられることを数学で証明しようと試みた。しかし、当初は簡単だと思われていたこの証明が難航を極める。結局、ケネス・アぺルとヴォルフガング・ハーケンの2人によって証明に成功したのは、100年以上経った1976年のことだった。

実は2人は数式ではなく、コンピュータを使って証明したのである。簡単にいうと、さまざまな図形のパターンを用意して、それをケース分けして、全部のケースについてコンピュータでしらみつぶしに検証したのである。

ロジカルシンキングの世界でよく使われる「ミーシー（MECE）」という言葉を、ご存じの方も多いはず。何か物事を分類するときに、「漏れなく、ダブりなく」分類するという考え方だ。

2人は平面図を、漏れなく、ダブりがないよう約2000通りに分類し、そのすべてのケースについてコンピュータで検証した。それも、4年の歳月をかけてである。ちなみに現在は、633通りまで分類を減らし、この四色定理は証明されている。

実はこの四色定理は、現実社会にも応用されている。たとえば、携帯電話のエリア配置。周波数の同じ携帯電話の基地局が隣接しないように、四色定理によってエリア分けを行っているのだ。