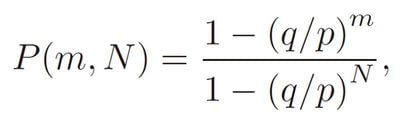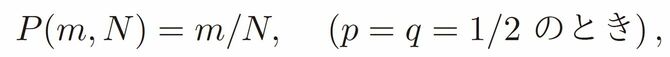大きな成功をした人は普通の人と何が違うのか。物理学者の大栗博司さんは「持って生まれた才能もあるが、積み重ねる確率をほんの少しずつ有利にするだけで長い目で見て大きな差がでることもある。これはギャンブルにも健康にも言えることだ」という――。

※本稿は、大栗博司『数学の言葉で世界を見たら』（幻冬舎新書）の一部を再編集したものです。

トランプ
写真＝iStock.com／okan akdeniz
※写真はイメージです
全ての画像を見る（5枚）

数学的に「ギャンブルで負けない方法」

「2つのことが独立に起きる確率は、おのおのの確率の積になる」という性質を応用して、ギャンブルで負けない方法を伝授しよう。

たとえば、コインを投げて表が出るか裏が出るかを賭けるとする。コインに癖がなければ、どちらの確率も1／2だ。癖がある場合も考えるために、表が出る確率をp、裏が出る確率をqとしよう。コインには表か裏かしかないから、この2つの確率にはp＋q＝1という関係がある。

表が出たら1円もらえて、裏が出たら1円取られるという賭けをする。2回連続して投げて、2回とも表になる確率はp×p＝p2。これをくり返すと、n回連続して投げてn回とも表になる確率はpnとなる（pnとはpをn回掛けるという意味で、pのn乗と読む）。

pは1より小さいのだから、nが大きくなると、pnはどんどん小さくなる。これは、連続して何回も勝つことは起きにくいという、常識的にも納得できる話だ。

さて、最初にm円持って、1円ずつ賭けていくとする。ギャンブルは引き時が肝心だというから、N円になったらやめることにしておこう。途中でやめず、目標のN円に到達するか、ゼロ円になって破産するまで続けることにする。

たった1％の違いで破産確率が急上昇する

勝って帰れる確率をP（m，N）と書くことにしよう。Pは英語で確率を意味する“Probability”の頭文字で、確率を表す記号によく使われる。m円で始めてN円になる確率だということを覚えておくために、（m，N）と書き添えた。確率が1／2より大きければ勝つ見込みがあるし、逆にあまり小さいようならやめておいたほうがよいということになる。この確率を計算すると、

計算式①
出所＝『数学の言葉で世界を見たら』（幻冬舎新書）

となる。

この公式は簡単に導けるけれど、少し長くなるので、僕のウェブページに置いた補遺で説明する。ただし、p＝q＝1／2のときには、q／p＝1なので、右辺の分子も分母もゼロになって、ゼロ÷ゼロと意味がなくなってしまうので、そのときだけは別に計算すると、

計算式②
出所＝『数学の言葉で世界を見たら』（幻冬舎新書）

となる。逆に、所持金ゼロ円になって破産して帰る確率は1－P（m，N）だ。

たとえば、p＝q＝1／2とすると、P（100，200）＝1／2。このときには、100円持ってギャンブルに行くと、持ち金を倍にして帰る確率と、破産してしまう確率は五分五分というわけだ。

さて、ギャンブルの胴元がコインにちょいと細工をして、p＝0.49、q＝0.51としたとしよう。このとき、上の公式を使ってみると、P（100，200）≒0.02となる。この計算については、第3話第3節で説明した。つまり、持ち金を倍にして帰れる確率は50回に1回になってしまう。98パーセントの確率で破産してしまうんだ。コインに1パーセントだけ裏が出やすい癖をつけただけなのに、破産する確率が50パーセントから98パーセントと激増したのだ。