課題を解くためのPOINT3:中央値とは
極端なデータの影響を回避するワザ
▼平均を使うときの落とし穴に注意
平均は便利なツールですが、その使用にはいくつかの注意点があります。
平均値とは「合計値を個数で割ったもの」ですが、そこにはどんな意味があるでしょうか。考えてみてください。
平均というと感覚的に「真ん中の値」「データ全体を代表する値」「最もデータの数が多い値」と考える人が少なからずいると思います。しかし、必ずしも平均がそうした特徴を常に持っているとは限りません。
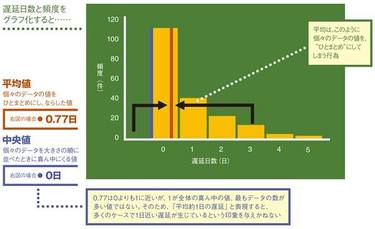
遅延日数と頻度をグラフ化すると……
前項で平均配達遅延日数は約0.77日と算出されました。しかしグラフ(図参照)を見ると、最も0.77に近い整数である「1日」は真ん中の値ではなく、全体を代表しているようにも見えず、最もデータの数が多い値でもありません。
なぜかというと平均とはあくまで合計値を個数で割ったものでしかなく、個々のデータの散らばり方とは何の関係もないからです。このデータの散らばり方を「分布」と呼びます。
ここに平均を使ううえでの注意点があります。平均は分布に関係なく複数のデータをひとまとめにならすため、個々のデータの特徴を消し去ってしまうという側面があります。平均を使うときはこの点に留意し、次の2つのポイントを常に頭に置いておくことが大切です。
(1)平均は常に分布の真ん中にあるとは限らない
(2)平均の周りに最も多くのデータが存在するとは限らない
このような平均というツールの限界には、いくつかの処方箋があります。(1)に対する処方箋が「中央値」です。
中央値とは、データをその値の大きさ順に並べたとき、ちょうど真ん中に位置する値のことです。「1、6、10、15、28」というデータの集まりであれば、真ん中の10が中央値になります。もし「1、6、10、15」のように偶数のデータの集まりなら、真ん中を挟む6と10の平均である8が中央値になります。
平均値を決める要素がデータの値の大きさであるのに対し、中央値を決めるのはデータの数です。中央値は大きさ順で並べた真ん中に位置するため、それより小さいデータと大きいデータの数は同じになります。平均と違い、例外的に極端な大きさを持つデータに引っ張られる影響を排除できます。
このような特徴を持つ中央値と平均値を比べて大きな差がなければ、データのばらつき方に極端な問題はないと考えられ、データの集まりの代表的な値として平均値を使っても大丈夫だろうと判断する1つの目安になります。

