｢日本人の平均所得が552万円というのは高すぎる｣そんな直感の正しさを裏付ける"平均のウソ" 実態は｢平均所得に届いていない人｣が大半

意外と知らない「偏差値」の中身

最後に標準偏差です。

「標準偏差」には、平均値からの散らばり具合という意味があります。

数学的には、分散の非負平方根でも求まります。

急に難解になったので、具体的な例を紹介します。

松本健太郎『データ分析力を育てる教室』（マイナビ出版）

全国統一模試における、わたしの得点が150点満点で70点だったとします。

ただし、平均点は80点でした。

「まぁ、惜しかったな」でしょうか、それとも「かなり点数は低い」でしょうか。

特に入試などの合否判定は、実際には得点では決まらず、上から数えて何人目の得点かで決まります。

自分の得点はどれくらいの位置にいるのかを知るのに適しているのが標準偏差です。

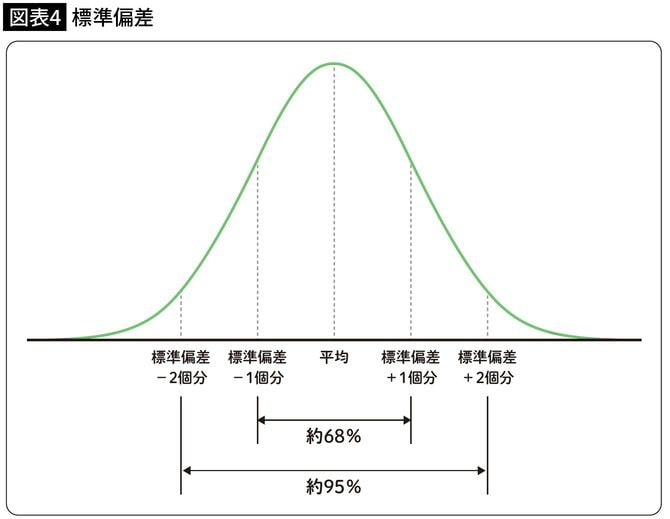
平均を中心に、±1個分の標準偏差で全体の68％、±2個分の標準偏差で全体の95％を占めます。

もし標準偏差が5点なら、70点は標準偏差－2個分、すなわち下位5％に該当するので、先にあげたわたしの得点では絶望的だとわかります（図表4）。

出所＝『データ分析力を育てる教室』

ちなみに試験で必ず求められる偏差値は「（得点－平均点）÷標準偏差×10＋50」で求まります。

わたしの場合、

となります。

模試を受けると大半の場合は偏差値もわかりますが、あれは全体における自分の学力の傾向を示していたのです。

偏差値を求めれば、仮に1回目の模試と2回目の模試が同じ得点でも、平均点が変動していれば偏差値も変動し、自分の学力がどれほどなのかを判断するのに役立ちます。