筆算不要の2ケタかけ算「桜井式」の手順 小6のときに発見した"法則"

たったの2ステップで終わる「2ケタのかけ算」の早業

私は子どものころから算数や数学の本質を考えることに喜びを感じてきた。小学6年生のときに、ある数を「9」で割る簡単な計算法を見つけた。今回は同じく小6のときに発見した、2ケタのかけ算（1□×1○、9□×9○）の簡単な解き方をご説明しよう。

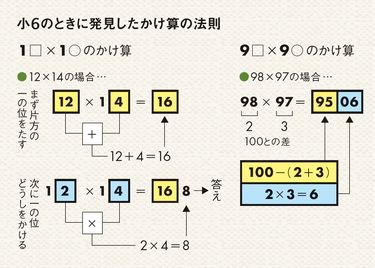
2ケタのかけ算は一般的に筆算で解くが、桜井式計算法では筆算は使わない。たったの2ステップで終わる。「12×14＝？」は、【1】前の数（12）と後ろの数の一の位（4）をたした数（12＋4＝16）が答えの百と十の位になり、【2】前の数の一の位（2）と後ろの数の一の位（4）をかけた数（2×4＝8）が答えの一の位になる。つまり答えは「168」だ。

もう1つ、（9□×9○）のかけ算はどうか。これは「100」との差を利用する。「98×97＝？」の場合、100との差が前の数は「100－98＝2」、後ろの数は「100－97＝3」。これを使い、上下2ケタずつ分けて答えを出す。上2ケタは、100に足りない数の和（2＋3＝5）を100からひいた数「100－5＝95」になる。下2ケタは、100に足りない数の積（2×3＝6）だ。つまり、「9506」が答え。

この2ケタのかけ算も数多くの問題（パターン）を並べ、それを見比べることで、共通する法則（ルール）を見出し、完成させたものだ。ビジネスの場でも、初対面の人と会話するとき、出身地や趣味など無意識に共通点を探しているはず。意識はしていないが、人間はみな数学的なのだ。