｢100年に1人の天才｣でも｢最新のAI｣でも解けない…使うのは＋×÷だけなのに世界中の数学者が敗北した難問 賞金は1億2000万円｡でもハマると人生を棒に振る

※本稿は、NHK「笑わない数学」制作班編『笑わない数学2』（KADOKAWA）の一部を再編集したものです。

写真＝iStock.com／Imgorthand

※写真はイメージです

全ての画像を見る（6枚）

賞金1億2000万円の「見た目が単純すぎる未解決問題」

好きな数を一つ思い浮かべてください。ただし、分数や小数、マイナスの数ではなく、1、2、3などの自然数でお願いします。その数に次の操作をし、その計算結果にさらにこの操作をし、……のようにどんどん繰り返してみてください。

この操作を十分な回数繰り返すと「1」になりましたね？　1にならなかった方はどこかで計算ミスをしている可能性が高いです。

「計算ミスをしている可能性が高い」と書きましたが、本当に必ず1になるかどうか、実はまだ証明されていない数学の未解決問題なのです。この問題は「コラッツ予想」と呼ばれています。まるで数遊びのような見た目をしたこの問題は、次の予想が正しいかどうかを証明する問題です。

問題の内容は小学生にもわかるのに、80年以上もの間、世界中の数学者の挑戦をはねのけ続けている超難問です。なんと、1億2千万円の懸賞金までかかっているのです。

ほんとうに1になるのか

この問題について考える前に、本当に1になるのかどうか、小さい数で試してみましょう。

まずは2から。2は偶数ですから、2で割って、1です。

3はどうでしょうか。3は奇数なので、3倍して1を足します。すると10になります。10は偶数なので、2で割ります。すると5。これは奇数なので3倍して1を足して、16。これは偶数なので2で割ると8、さらに2で割ると4、さらに2で割って2、さらに2で割って1になります。

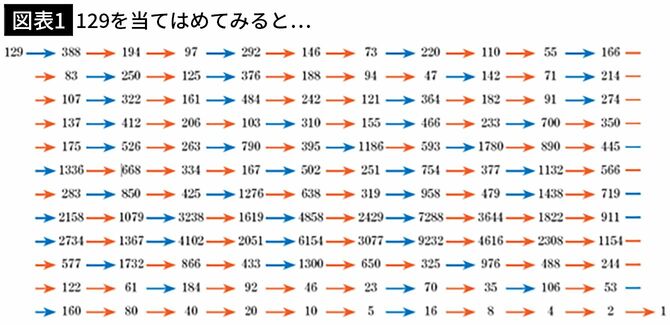
では、少し大きな数にもチャレンジしてみましょう。例えば、129は次のように変化します。

『笑わない数学2』より

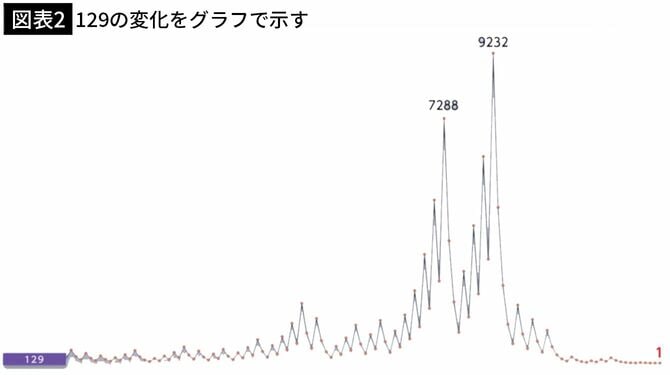
グラフにするとこんな感じ。

『笑わない数学2』より

121回の操作で1になります。その間に9232まで値が大きくなっていますが、なんとか1になっています。これだけ大きい値になっても最終的にはちゃんと1になりましたね。

では、どんな自然数でも、最終的には1になるのでしょうか？

現在では、コンピュータを使ってものすごく大きな数まで1になることが確かめられています。最新の研究の一つによると、17垓7088京7431兆761億1695万5136以下の自然数はすべて、1になることがわかっています。

ここまで確かめたのなら、もうコラッツ予想は正しい！　と言いたいのですが……残念ながら、これよりも大きな自然数は無限にあります。ですから、ここまで確かめても、コラッツ予想が正しいとは言い切れないのです。

つまり、コラッツ予想を証明するには、なんらかの方法で、無限個の自然数が1になることを一気に示す必要があるのです。