数学的には誰が当選してもおかしくない
ニコラ・ド・コンドルセ(Nicola de Condorcet)という人がつくった投票方式を利用すれば、また別の結果が出ます。
彼が考案したコンドルセ方式は「一対比較(pairwise comparison)」とも言われます。
何人かの候補のうち2人ずつ組み合わせ、どちらかに投票することを繰り返していきます。そしてすべてのペアを1対1で比較した結果を統合する方法です。
これも一度やってみると、すぐに理解できるでしょう。AからEまで5人の選好度表を見ながら、一対比較をしてみましょう。5人の候補がそれぞれ別の候補と一度ずつ一対比較をするには、何回投票をすればいいでしょうか?
5×4÷2=10で、10回の投票をすればいいですね。
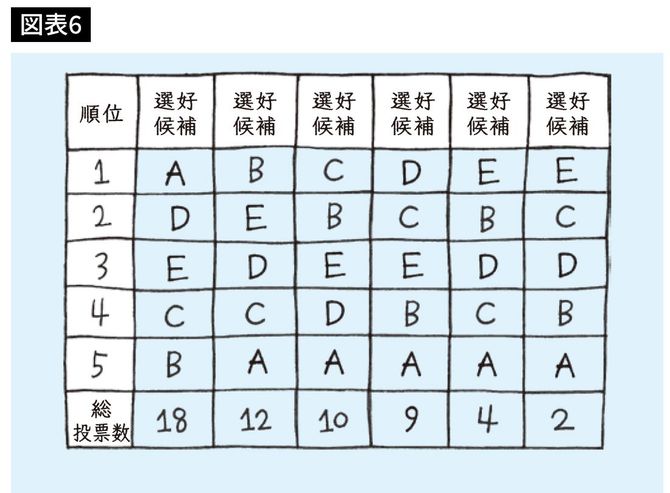
わかりやすいように、選好度表(図表6)をもう一度見てみましょう。
まずAとBを比較すると、どちらが勝つでしょうか? 他の人たちはすべて除いて、2人だけを比べます。BよりAの方が好きな人は18人しかいません。A対Bで見ると、18:37で圧倒的にBの勝ちです。
Aは1対1で比較すると、全員に負けます。
では、Aを除いてB対Cを比較してみましょう。Cを選好する投票は18+10+9+2 =39で、CがBに勝ちます。CとDを比べると、Dが43票でDが勝ち、DとEを比べると27:28で僅差ですがEが勝ちます。Eがかなり優勢に見えますね。
E:B=33:22
E:C=36:19
E:D=28:27
上の結果を見ると、1対1で比較したとき、誰と比較してもEの選好度が高いので、Eが勝つことになります。かなり説得力のある論理ではありませんか?
このように誰と比較しても勝つ候補がいる場合、コンドルセ勝者(Condorcet’s winner)と呼びます。そこでコンドルセの原理を「コンドルセ勝者がいれば、その候補が勝つべきだ」と表現することもあります。
1対1の比較をして選好度の高い候補がいれば、その人が勝つべきだということですが、はたしてそんな候補がいるでしょうか? いないこともあるでしょう。
実際、コンドルセ方式は現実の選挙の方法論とは言いがたいものです。投票したら誰かが勝者にならないといけないのですが、勝者がいないこともあるからです。
つまり、これまで出てきた方法論には、いずれも頭の痛い欠点があるようです。
社会的決定の問題がそれだけ複雑だということが、数学的にも表れています。
誰もが納得できる選挙に必要な3つの条件
1950年代、社会的決定システムが備えるべき非常に簡単な条件、誰が見ても理解できる3つの原則がつくられました。方法論ではなく、原則を羅列したものです。
第一の原則は、「意見一致の原則」です。もし、すべての人がBよりAを選好するなら、共同決定もやはりBよりAを選好すべきというものです。この第一の原則は、あまりに当然のことですよね。
第二の原則は、先ほどの「計算コンドルセ方式」からくるもので、「独立性の原則」です。これは、AとBの選好度の結果が、他の候補の有無によって変わってはならないというものです。CがいるときはAが勝ったのに、CがいないとBが勝つという状況になれば、社会が個人の合意からなるという理念に反します。
最後の原則は、ある一個人の意見がつねに社会的決定に反映されるような状況があってはならないというものです。投票を左右する「独裁者は存在しない」。この原則はよく理解できます。
意見一致の原則、独立性の原則、独裁者は存在しない。
この社会選択の三原則は、私たちが理性的だと感じる方法論の制約条件です。この原則さえ守れば、すべての人を満足させる方法論をつくることができるでしょう。