「しかも」「ゆえに」のような論理コトバで事実をつなげる
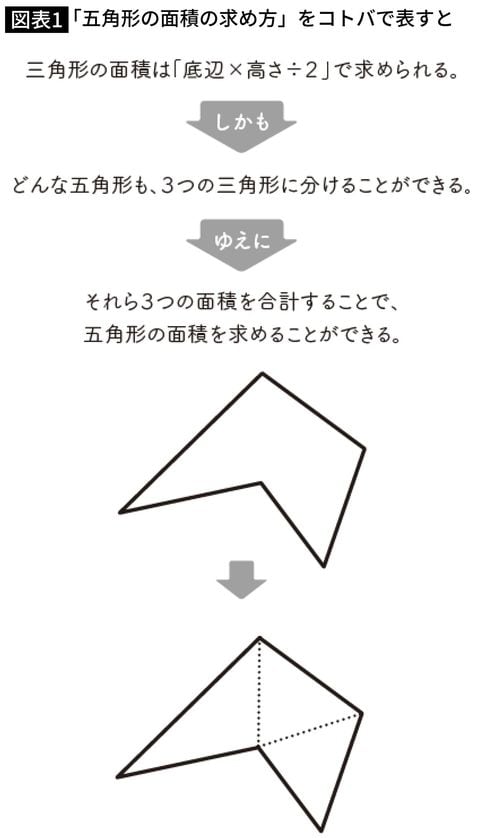
たとえば、五角形の面積をどう求めるか考えてみます(図表1参照)。
「しかも」や「ゆえに」のような論理的なコトバ(矢印➡で表現)で事実をつなげていくことで、五角形の面積を求める手法を説明できました。
「論理的なコトバ」という表現はちょっとカタいかもしれません。少し柔らかく「論理コトバ」と表現することにします。
ここからが重要です。もしあなたが学生だったら、このあとに実際に面積を計算し正解を求める行為をするわけです。でもよく考えてみてください。その計算という行為は単なる作業です。果たして数学という学問において、計算という作業は重要なことでしょうか。
いいえ。
重要なのは計算を正確にすることではなく、その前に論理コトバを使って問題の構造を把握した行為ではないでしょうか。
要するに、計算するという行為は数学のほんの脇役にすぎないのです。はっきり言いましょう。なくても困らないものです。
これが、数学とはコトバの使い方を学ぶ学問であるという私の主張の根拠です。
数学≠計算する学問
数学=論理コトバを使う学問
これが本当の数学の姿なのです。
余談ですが、いま大学生などは就職活動のときに能力検査のようなものを受検します。パスしないと面接などの採用活動に進めないのですが、能力検査の中には「言語」と「非言語」に概念を分け、別々に実施するものもあるようです。
「言語」はいわゆる国語。「非言語」がいわゆる算数や数学など数的思考力を確認するものとされています。
数学をコトバの学問と定義している私には、当然ながらこの分け方に納得できないでいます(苦笑)。どちらもコトバを扱う検査です。どうしても分けたいのなら、「国語力」と「数字力」といった名称にしてもらいたいと思うのですが……。
これ以上続けるとさらに脱線してしまいます。次に進みましょう。
自分ではわかっていても誰かに説明できない
私の主張にご納得いただくためには、もう少し説明が必要な気がしています。何しろ、私たちは数学の授業で相当量の計算をさせられてきましたからね。
そこで、ふたつほど具体的なエピソードをご紹介することにします。
まずひとつ目。
企業研修や大学の講義など教育の現場にいて、痛切に感じることがあります。自分ではわかっているのに誰かに説明することができない人の多さです。
要するに、こういうことです。
論理コトバを使ってものごとの構造を把握し、論証し、第三者にわかりやすく説明する行為ができない。
たとえば、机上では問題をスラスラ解くのに、ホワイトボードや黒板を使って説明してほしいと要求すると、強く拒否する学生がいます。理由は、「先生の説明をふまえてなんとなく『雰囲気』で解いた結果なので、正解かどうか自信がないから」だと言うのです。
あるいは、「自分では理解できているんですけど、部下に説明するのが難しくて」という悩みを抱えているビジネスパーソンも少なくありません。興味深いのは、数学の勉強がとてもできたはずの理系出身の優秀なビジネスパーソンの多くが、意外に説明やプレゼンテーションが下手だということです。あくまで私の経験からくる感覚値ですが。
いくら数学の成績がよかったとしても、これでは数学を役立てられていないと言えるでしょう。
なぜ、彼らは数学を役立てられていないのか。
それはかつての授業で「作業」しかしなかったからです。作業だけさせ、○×を与えるだけの教え方は、こういう大人をつくってしまうのです。