今回はゲーム理論の「交互ゲーム」を取り上げたい。交互ゲームは将棋や碁のように相手の打った手を見ながら、どの戦略を選ぶかというゲームだ。

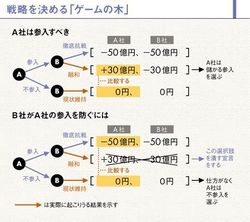
次のケースで考えてみよう。「家電メーカーのA社とB社がある。A社は白物家電、B社は音響製品に強みを持つ。ところが最近、A社が収益拡大を狙い、新たに音響関連市場への参入を検討し始めた。実際にA社が参入してきた場合、B社が取る戦略は基本的に2つだ。A社に対し徹底抗戦するか、あるいは融和策を取るかである。B社が徹底抗戦すれば、熾烈な価格競争に陥り、両社ともに50億円の損失が出る。一方、B社が融和を選択すれば、B社はシェアを奪われ30億円の損失が出る。逆に、A社は30億円の利益が生まれる。この場合、A社は音響関連市場に参入すべきか」――。

図を拡大
戦略を決める「ゲームの木」

交互ゲームでは、図のような樹形図（別名「ゲームの木」）をつくる。考えられるすべてのケースを時系列に沿って（起こる順に）書き、最後にそれぞれのプレーヤーの利得を書き込む。次に、後手の立場から「実際に起こりうる結果」を考えていく。今回の場合はB社が後手になる。

A社が市場参入した場合、B社は融和を選ぶはず。徹底抗戦すれば50億円の損失が出るのに対し、30億円の損失ですむからだ。また、A社が不参入の場合は、B社は現状維持で、両社ともに収益の増減はない。つまり、実際に起こりうるのは、「A参入＆B融和」または「A不参入＆B現状維持」のいずれかになる。A社の立場でこの2つの選択肢を考えると、当然、参入して30億円の利益を得たほうがいい。

さて、ここで気になるのは、これだとB社は「やられ損」ではないかということだ。B社がA社の参入を防ぐ方法はないのか。実はある。B社があらかじめ「徹底抗戦する」と宣言しておけばよいのだ。そうすれば、ゲームの木は図のようになる。A社が参入すれば、B社の徹底抗戦に遭い、B社も痛手を被るが、A社も50億円の損失が出る。したがって、A社は不参入の道を選択するほうが得だと判断するはずである。

実は、これと同じ構造が国際政治の場でもあった。米ソ冷戦時代のキューバ危機だ。1962年、旧ソ連がキューバにミサイル基地を建設し、米国に対して「いつでも攻撃をしかける用意がある」という態度を示したとき、当時のケネディ米大統領は「全面核戦争もやむなし」と徹底抗戦の構えをみせた。攻撃に甘んじるという選択肢をつぶすことで、結果、核戦争という最悪の事態を回避したのだ。

こうした駆け引きは、ビジネスの世界でも常に起こっているはずだ。ゲーム理論は、ビジネスにも有効な考え方なのである。

（構成＝田之上 信）