相手を説得したいなら｢お得ですよ｣は使ってはいけない…頭のいい人が使う心理に訴える｢鉄板フレーズ｣ 金額はそのままに｢いかにお得に見せるか｣

金額が大きくなるほど、感覚は麻痺する

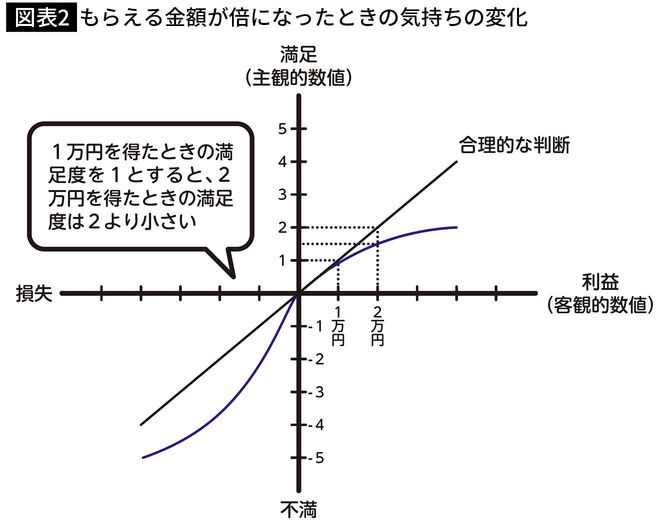
プロスペクト理論では「金額の大きさと、主観的に感じる価値は一致しない。金額が2倍になると、主観的に感じる価値は2倍にはならず、2倍弱（1.6倍ぐらい）になる」ということもわかっています。

「金額の絶対値が大きくなるほど感覚が鈍感になる」ということです。大きな買い物ほど、金銭感覚が麻痺してしまうことです。

出所＝『はじめての統計学 レジの行列が早く進むのは、どっち⁉』

図表2は、人がお金に関わる意思決定をするときに、頭の中でどういった計算が行われているのかを図式化したものです。S字の形をした線を「価値関数」といいます。

数学の授業に出てくる一次関数とか二次関数は、中学生のときに確か勉強しました。「関数」というのは、数値の変換装置のことです。何かの数値を入れると、別の何かの数値に変換してくれるものです。

価値関数は、「客観的な数値（金額）を人間の主観的な数値（価値）に変換する装置のことだ」と思ってください。この価値関数をもとに、「この金額はお得なのかどうか」を判断している、ということです。

もし合理的な選択をしているのであれば、客観的な数値（金額）と主観的な数値（価値）が一致するはずです。

しかし、人は必ずしも客観的で合理的な選択をしているわけではなく、どちらかといえば主観的な価値感覚を頼りに、「なんとなく」選択をしています。

人は客観的な数値をそのまま正しくとらえているのではありません。「金額」という客観的な情報を価値関数という変換装置にいったん入れて、心理的なインパクト（主観的数値）に変換してから判断しているということです。

図表2では横軸が「金額」、縦軸が「価値」です。横軸ではなく縦軸で判断しているということです。

いち消費者としては、金額そのものではなく、主観的な価値で判断していることを自覚していなければ、「いつの間にかお金がない」ということになりかねません。

金額はそのままに「いかにお得に見せるか」

一方で、マーケティングで重要なのは、金額という客観的なものさしを操作することではなく、人が実際に感じる「価値」という主観的なものさしを操作することです。

安易に「高いから売れないんだ、値下げしよう」というのは、客観的なものさしを操作しているにすぎず、あまり良い選択とはいえません。金額はそのままに、「いかにお得に見せるか」を考えたほうがいいでしょう。

プロスペクト理論は、私たちの日常のあらゆる場面に密ひそかに存在しています。

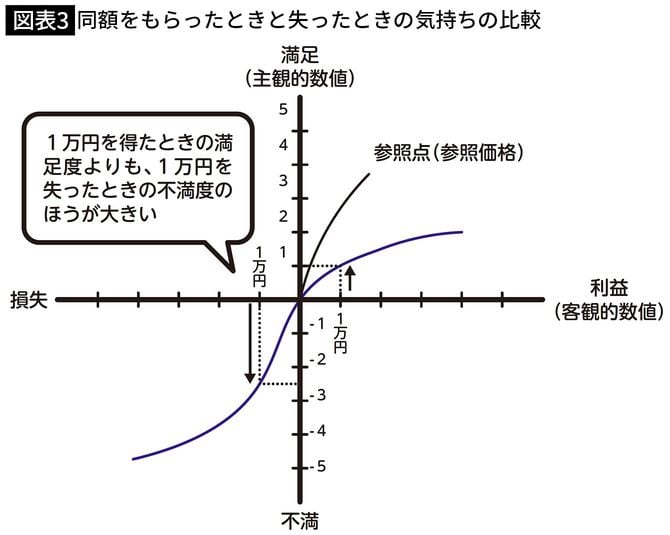
先ほどの「得をするよりも損を避けたい」損失回避バイアスについても、この価値関数で説明することができます。

出所＝『はじめての統計学 レジの行列が早く進むのは、どっち⁉』

1万円を得たとき（得をする）の嬉しさ（主観的な数値）が1だとすると、1万円を失ったときの悲しさ（主観的な数値）は2倍以上になっています（図表3）。

また、横軸と縦軸のクロスする箇所は、「参照価格」や「参照点」といわれています。これを説明するために、再びダニエル・カーネマンの実験を紹介します。

この実験の意味するところは、総額140ドルから5ドル安くなるという状況は、〈実験1〉も〈実験2〉も変わらないのに、

B：15ドル→10ドルで、33％値引き
C：125ドル→120ドルで、4％値引き

では、値引き率の大きいBのほうが魅力的に見える（わざわざ自転車で20分走ってもいいと思える）ということになります。

Bの場合の参照価格（基準となる価格）は15ドルで、そこからの変化の大きさ（値引き率）が33％。
Cの場合の参照価格（基準となる価格）は125ドルで、そこからの変化の大きさ（値引き率）が4％。

どちらも−5ドルで値引き額は同じでも、値引き率で「お得かどうか」を判断しているということです。

例えば、100万円の車を1万円引きされてもあまり嬉しくないのに、スーパーの買い物では、数十円～数百円安くなっているだけでも嬉しく感じます。でも本当は、高い買い物ほど値切れるだけ値切ったほうがいいはずです。