※本稿は、サトウマイ『はじめての統計学 レジの行列が早く進むのは、どっち⁉』(総合法令出版)の一部を再編集したものです。
期待値が同じでも「もらえる」「失う」で回答率が変わる
突然ですが、次の2つの質問に直感で答えてください。
〈質問1〉どちらのくじを選びますか?
A:90万円もらえる確率が100%のくじ
B:100万円もらえる確率が90%のくじ
〈質問2〉どちらのくじを選びますか?
A:90万円を失う確率が100%のくじ
B:100万円を失う確率が90%のくじ
「直感で選んでください」といっておきながら、どちらを選ぶのが数学的に正しいのかを先に検証してみたいと思います。
客観的な正しさは、本書の第2章で解説した「期待値」を計算します。期待値とは「1回くじを引いたときの、取りうる値の平均値」です。この値の高いほうを選ぶ、ということです。
期待値の計算は、
取りうる値×その値を取る確率(の合計)
で求められます。それでは計算してみましょう。
〈質問1〉
Aのクジの期待値=90万円×1(100%)=90万円
Bのクジの期待値=100万円×0.9(90%)=90万円
〈結果〉
AもBも同じ期待値(数学的な正しさは一緒)
〈質問2〉
Aのくじの期待値=−90万円×1(100%)=−90万円
Bのくじの期待値=−100万円×0.9(90%=−90万円
〈結果〉
AもBも同じ期待値(数学的な正しさは一緒)
期待値が同じで、回答者の属性に偏りがなく(例えば主婦層だけなど)、幅広い属性がランダムに選ばれているのであれば、あとは好みの問題で、AとBに半々くらいに分かれるはずです。
しかし、〈質問1〉ではAを選ぶ人が多くて、〈質問2〉ではBのほうが多いというように、“選択の好み”に偏りが出ることがわかっています。
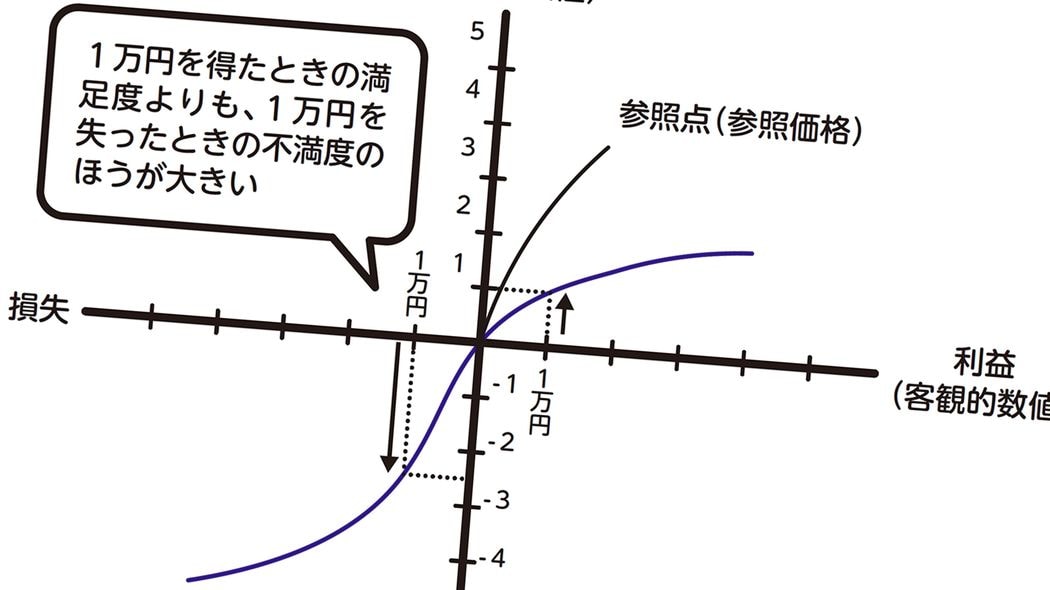
「もらえる」といったときは確実なほう(確率100%)を選ぶのに、「失う」といったときはリスクを取る(100%でない)人が多いのです。これを「プロスペクト理論」といいます。