平均気温が低い地域ほど、雪日数が多くなるのは「負の相関」
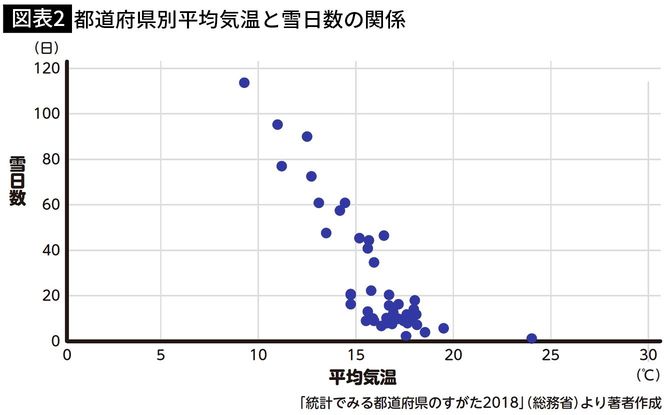
図表2は、2016年の各都道府県の年間平均気温と雪日数の散布図です。見ると、右肩下がりのグラフになっています。これは平均気温が低い地域ほど、雪日数が多くなるためです。
このように、一方が下がると、もう一方が上がるような関係を「負の相関」といいます。「相関がない」場合には、2つの値には「なんらかの結びつきがあるとはいえない」と考えます。
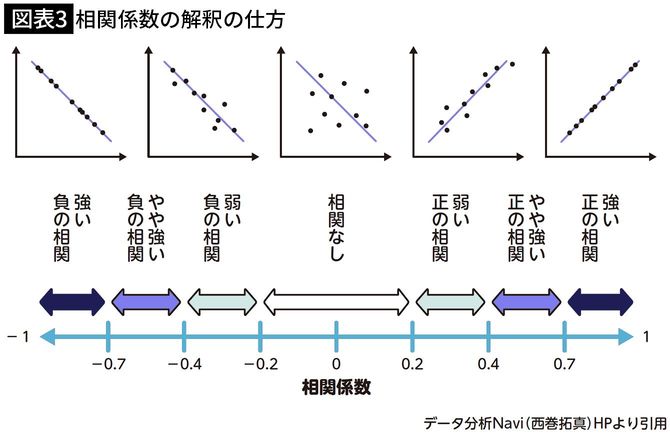
2つの値の関係性の度合いを表す指標を「相関係数」といいます。相関係数は、−1~1の値で表され、関係性が強い値ほど絶対値が1に近づきます(図表3)。
一般的には、相関係数が0.5以上であれば、相関が強いと判断されることが多いです。
これはどのくらいの関係性の強さかというと、「親の身長と子どもの身長の相関係数」がだいたい0.4~0.5といわれています。
相関係数の値は、エクセル関数ひとつでも簡単に計算することができますが、その分、解釈を間違える人がかなり多いのです。
相関を使って人を騙す方法
冒頭のクイズで出した3つの例は、「2つの値の相関が強いもの」です。
しかし、相関関係にあるからといって、それは「因果関係になっているとは限らない」ということに注意が必要です。
例えば、
ここで出てくる2つの数値は、以下の通りです。
・その地域の警察官の数
・その地域の犯罪件数
確かに、両者は相関関係にあるものの、「警察官の数(原因)→犯罪件数(結果)」という関係性にはなってはいません(完全に因果関係がないといいきることはできませんが、論理的に考えるとおかしい)。
「その地域の人口」という見えない第三の変数が、両者の本当の原因なのです。
②アイスが売れる日は、水辺で事故がよく起きる
③体重が重い小学生ほど、足が速い
も同様に、それぞれ「季節(気温)」「学年(年齢)」が、第三の変数です。
このように、見えない第三の変数のことを「潜伏変数」といいます。潜伏変数によって、単なる相関関係を因果関係と見誤ることがよくあり(錯誤相関)、この関係を「見かけの相関」や「疑似相関」といいます。
統計に明るくない人は、相関関係と因果関係を混同して説明しているときがあるので気をつけましょう(相関関係と因果関係を明確に区別して説明しているビジネスパーソンのほうが少ない、という感覚を持っています)。