データとしては正しくても解釈が違う

まずひとつ目の「警察官が多い地域は、犯罪件数が多い」ですが、データとしては「正しい」です。

では、「警察官を減らせば、犯罪は減るということ？」という解釈は正しいでしょうか？　答えは「ノー」です。

こういったデータになる理由のひとつに、「人口が多い地域ほど警察官は多い。人口が多い地域ほど犯罪件数は多い。よって、警察官が多い地域は犯罪件数が多くなる」ということです。

これは、本書で説明している「毎年あの宝くじ売り場で高額当せんが出るのは本当なのか」が数学法則としては正しいが、当たる数と当たる確率は別物である、という話と同じです。

2つ目の例、「アイスが売れる日は、水辺で事故がよく起きる」ですが、こちらもデータとしては「正しい」です。

では、「アイスを売らなければ、水辺での事故は減る」のでしょうか？　答えは「ノー」です。

アイスがよく売れる日というのは夏場です。夏場は、海水浴や川遊び、プールなどへ出かける人が多いため、水辺の事故の件数が多くなります。アイスの販売を規制したからといって、事故の抑止にはつながらないでしょう。

本当の原因ではないものを操作しても、結果には影響しない

3つ目の例、「体重が重い小学生ほど、足が速い」ですが、こちらもデータとしては「正しい」です。

では、「たくさん食べて太れば、足が速くなるのでは？」という解釈は正しいでしょうか？　答えは「ノー」です。

体重が重い児童は、高学年に多いですよね。高学年の児童は、低学年の児童よりも足が速いです。したがって、「体重が重い小学生ほど、足が速い」という関係になるということです。

わかりましたか？　ひとつ目の例では、「人口」が、2つ目の例では「季節（気温）」が、3つ目の例では「学年（年齢）」が、本当の原因として隠れていました。本当の原因ではないものを操作しても、結果には影響しないのです。

このように、相関関係を因果関係と混同してしまうことを「錯誤相関さくごそうかん」といいます。

【図表1】身長と体重の関係
出所＝『はじめての統計学 レジの行列が早く進むのは、どっち⁉』

相関というのは、2つの値の関係性のことです。

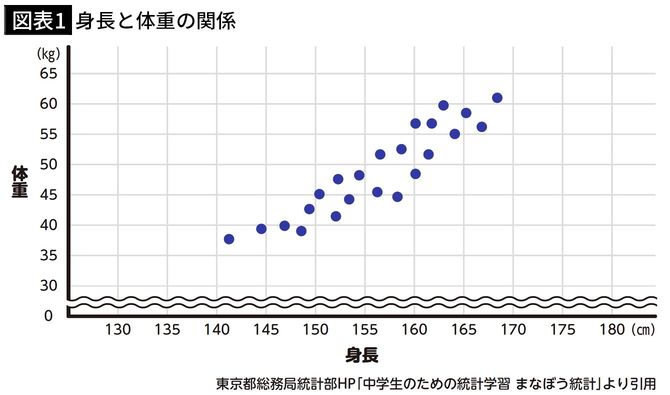
例えば、身長と体重は相関関係です。身長が高い人ほど、体重が重くなります。身長と体重の散布図を描くと図表1のようになります。直線的に右肩上がりになっているのがわかるでしょうか？

これを「正の相関」といいます。一方が増えると、もう一方も増えるような関係性です。