わからない時は「図を描く」のが難問との戦い方
とてもメールでは済まなそうな内容なので、大澤教頭先生のご厚意に甘えて、私は再度、学習院初等科にお邪魔した。
先生は快く迎えてくれた。そして、順序立てて、「謎解き」をしてくれた。
正対する、算数のカリスマ先生と算数オンチの私。スペシャルな“個別授業”はまず正○角形の定義の確認から始まった。正○角形とは、辺の長さがすべて同じで、内角の大きさもすべて等しい図形だ。ということは、正○角形の○の数値によって内角の角度も変わるということで、その角度がわかれば「答え」を導くことができるかもしれない。
ただし、答えは導けるかもしれないけれど、じゃあ、角度はどう出せば……? と考えあぐねている私に、先生は正5角形を描いて考えてみることを提案してくれた。わからない時は、まず図や絵で描いてみること。名教師が、口を揃える、難問との戦い方だ。
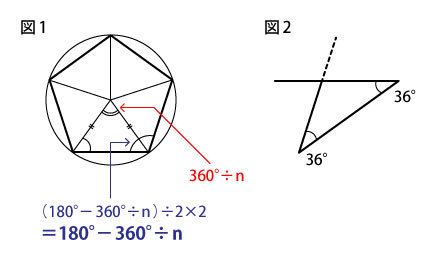
さて、図1を参照してほしい。
正5角形を描いてみると、中に二等辺三角形が5つ入っていることがわかる。二等辺三角形の頂角は「360°÷5」だ。次に底角は、三角形の内角の和180°から頂角を引いて、2で割った(180°-360°÷5)÷2で算出できる。正五角形の内角は、この底角2つぶんになっているから、(180°-360°÷5)÷2×2となる。÷2×2は打消しあっているので、カット。これを正n角形に置き換えると、次のような式になる。
180°-360°÷n
ずいぶんシンプルになった。nに正3角形の「3」を入れて計算してみると、おお、確かに60度になる。正4角形(正方形)の「4」を入れたら、うん、90度だ。正しい。この公式は完璧ですね、先生!
でも……正3角形や正4角形は直感的に図形がイメージできるけれど、正2.5角形の場合ができない。果たして、公式は成立するのか? ちょっとドキドキしながら「2.5」を入れて計算してみると、36°だ。お、割り切れた。では、本当に図形を描けるのか? 期待に胸がふくらむ私。ほとんど未知との遭遇だ。
まず、適当な長さで一辺を描く。とりあえず、5cmとしよう。そして、分度器で36°の角度をとって、5cmを引く。さらに36°の角度をとって線を引くと……最初に書いた線にぶつかってしまう。ここで手がとまる(図2)。あーあ、やっぱり図形なんてできないじゃん。心の中でつぶやく。
「どうしましょう?」と大澤教頭。
どうしましょう? って……。万事休すですよ、先生。算数オンチの私にできるのはここまで。だが、先生はここで、「内角はすべて同じ」以外の正○角形の約束をもう一度思い出してほしいと言った。
えっと、辺の長さはすべて同じ、でしたっけ。
「そうですね。では、線と線がぶつかることは気にせず、書いてみましょう」
は、はい。ということで淡々と36°の角度をとって、5cmの辺を引いた。線と線が何度も交差した。そして最終的に現れた図形を見て、はっと息をのんだ(次ページ図3)。