Q2 逆さにした3つのカップa、b、cのうち1つには菓子が入っています。エミさんはcのカップに菓子が入っていると予想しました。すると、正解を知っているお父さんは、「aには菓子が入っていないよ」と教えてくれました。エミさんは予想をbに変えたほうがいいか、cのままでいたほうがいいか、当たる確率が高いのはどちら?
A 三つあるカップのうち、当たりは一つだけ。エミさんがcを選んだ後で、答えを知っているお父さんが「aは違う」と教えてしまう。とすれば正解はbかcになり、確率はどちらも2分の1。選び直してもそのままでも当たる確率は変わらない。そう考えた人はいませんか。
これは数学関係者の間では非常に有名なモンティ・ホール問題といわれる問題です。名前の由来は、1970年代にアメリカで人気を誇ったゲームショー番組の司会者名です。講演会などで私はよくこの話をしますが、95%の人は選択を変えません。最初の直感を信じたいからや、2択で確率は50%だから、どちらを選んでも同じ、というのがその理由です。
ところが、変えたほうが当たる確率は2倍になるのです。答えを言うと、当たる確率は変えた場合が3分の2、変えない場合が3分の1。これについてはアメリカの学者間でも論争になり、実験の結果、証明されました。
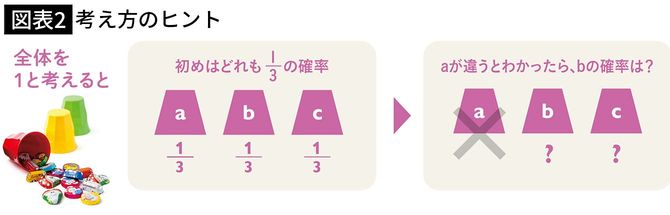
なぜ変えると当たる確率が上がるのか。エミさんが初めにcのカップを選んだときの確率は3分の1です。そのとき選ばなかったほうが当たる確率は3分の2。これらをグループで考えると、3分の2のグループのカップ(a、b)が一つは空とわかったところで、そのグループの確率は変わらないのです。
それでもいまひとつ釈然としないようであれば、カップを10個に増やして考えてみるといいでしょう。最初に選んだときに当たる確率は10分の1、選ばなかったほうは10分の9。選ばなかった9個のカップのうち、外れのカップを順番に一つずつ開けていきます。カップ一つだけを残して。そうすると、その一つに自分が選ばなかった10分の9が集約されていることが自然とわかるはずです。(答え bに変える)