「大数の法則」を制する者は賭けを制す

多くのスポーツでは、数回戦のゲームを行って総合的に勝敗をつけるようなルールになっています。

なぜなら、1回の勝負だけでは運よく勝つこともあるかもしれませんが、数回戦の長期戦のゲームになれば本当に実力のあるチームが勝つはず、という統計的な前提に基づいているためです。

じゃんけんであれば、「本当の実力＝各手の勝率」ということです。

自分が「グー」を出して勝つ確率：31.7％
自分が「チョキ」を出して勝つ確率：33.3％
自分が「パー」を出して勝つ確率：35.0％

潜在的な勝率に偏りがあれば、長期戦にすることによって本当の実力がデータに表れやすいことを「大数の法則」といいます。

サイコロを例に、大数の法則について紹介します。

サイコロの目1～6までの各数字は、それぞれ、1／6の確率で出現します。1／6は16.67％くらいです。

「16.67％」というのが、各数字が出現する「本当の実力」を表していると考えてください。

この場合、歪ゆがみのないサイコロなので、「1～6の各数字の本当の実力は16.67％ですべて等しい」ということになります。この状態を確率の世界では、「同様に確からしい」といいます。

各出目が出る確率は、理論上は等しくても、例えば、サイコロを6回投げたとき、1～6までの数字が必ず1回ずつ出るとは限りません。もしかすると、1の目が6回続くかもしれません。

試行回数が多いほど、「本当の実力」に収束

確率現象を実験したり観察したりすることを「試行」といいます。

サイコロを振る回数（試行回数）を12回に増やしたとして、1～6までの各数字が出る回数の期待値はいくつになるでしょうか？

12回×1／6＝2

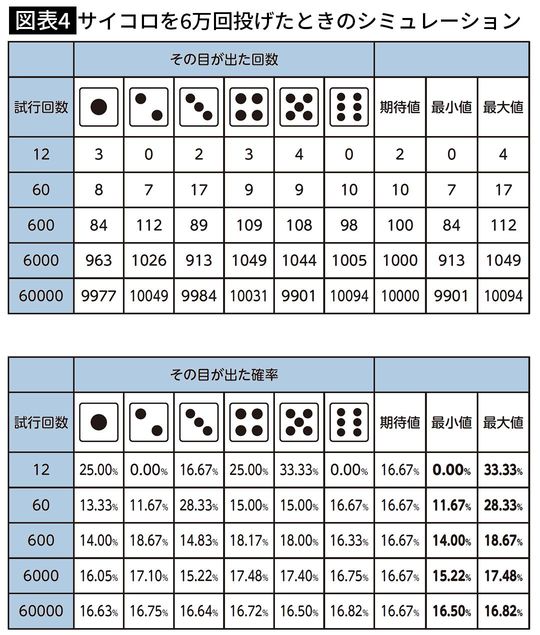
で12回サイコロを振ったら、1～6までそれぞれ2回ずつ出る計算になります。実際にコンピューターでシミュレーションをすると、図表4のような結果になりました。

各出目が出る回数の期待値は2回のはずですが、2と6の目は1回も出ていない一方で、5の目は4回も出ていますね。各出目の出現確率も0～33.3％とバラついています。

ではこれを、60回、600回、6000回、6万回と試行回数を増やすと、どういった結果になるか見てみましょう。

60回もサイコロを振れば「1回もその目が出なかった」ということはなくなりましたが、出現確率は11.7～28.3％とまだバラつきがあります。

600回では出現確率が14～18.7％となり、バラつきが小さくなってきました。

さらに、6000回では出現確率が15.2～17.5％となり、もっとバラつきが小さくなってきました。

【図表4】サイコロを6万回投げたときのシミュレーション
出所＝『はじめての統計学 レジの行列が早く進むのは、どっち⁉』

そして、6万回では出現確率が16.5～16.8％になり、どの出目も「本当の実力」である16.67％付近に落ち着いているのがわかります。

出現確率の変化に注目してほしいのですが、試行回数が60回、600回、6000回、6万回と多くなるごとに各出目の出現確率にブレが少なくなっているのがわかると思います。

試行回数が多いほど、「本当の実力」（16.67％）に収束していく大数の法則が働いているためです。